
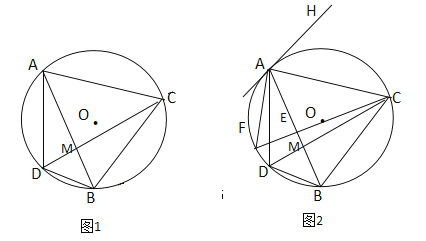
【题目】如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.
(1)求证:AC=BC;
(2)如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;
(3)在(2)的条件下,若ΔABD的面积为![]() ,ΔABD与ΔABC的面积比为2:9,求CD的长.
,ΔABD与ΔABC的面积比为2:9,求CD的长.
【答案】(1)证明见解析;(2)30°;(3)![]()
【解析】
(1)运用“在同圆或等圆中,弧相等,所对的弦相等”可求解;
(2)连接AO并延长交BC于I交⊙O于J,由AH是⊙O的切线且AH∥BC得AI⊥BC,易证∠IAC=30°,故可得∠ABC=60°=∠F=∠ACB,由CF是直径可得∠ACF的度数;
(3)过点D作DG⊥AB ,连接AO,知ABC为等边三角形,求出AB、AE的长,在RtΔAEO中,求出AO的长,得CF的长,再求DG 的长,运用勾股定理易求CD的长.
(1)∵DC平分∠ADB,∴∠ADC=∠BDC, ∴AC=BC.
(2)如图,连接AO并延长交BC于I交⊙O于J

∵AH是⊙O的切线且AH∥BC,
∴AI⊥BC,
∴BI=IC,
∵AC=BC,
∴IC=![]() AC,
AC,
∴∠IAC=30°,
∴∠ABC=60°=∠F=∠ACB.
∵FC是直径,
∴∠FAC=90°,
∴∠ACF=180°-90°-60°=30°.
(3)过点D作![]() ,连接AO
,连接AO

由(1)(2)知ABC为等边三角形
∵∠ACF=30°,
∴![]() ,
,
∴AE=BE,
∴![]() ,
,
∴AB=![]() ,
,
∴![]() .
.
在RtΔAEO中,设EO=x,则AO=2x,
∴![]() ,
,
∴![]() ,
,
∴x=6,⊙O的半径为6,
∴CF=12.
∵![]() ,
,
∴DG=2.
如图,过点D作![]() ,连接OD.
,连接OD.
∵![]() ,
,![]() ,
,
∴CF//DG,
∴四边形G′DGE为矩形,
∴![]() ,
,
![]() ,
,
在RtΔ![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
【题目】(![]() )如图
)如图![]() ,
,![]() 中,
中,![]() ,
,![]() 是
是![]() 上任意一点,以点
上任意一点,以点![]() 为中心,取旋转角等于
为中心,取旋转角等于![]() ,把
,把![]() 逆时针旋转,画出旋转后的图形.
逆时针旋转,画出旋转后的图形.
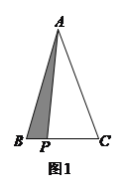
(![]() )如图
)如图![]() ,等边
,等边![]() 中,
中,![]() 为
为![]() 边上一点,
边上一点,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
求证:![]() .
.
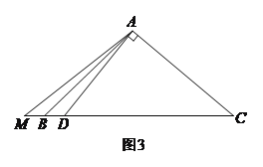
(![]() )已知:如图
)已知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,已知
,已知![]() ,
,![]() .写出求线段
.写出求线段![]() 长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.
长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
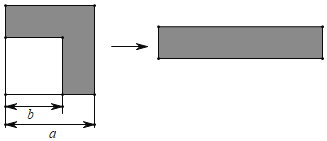
【题目】如图,在边长为a的正方形的一角剪去一个边长为b的正方形,把剩余的部分(图中的阴影部分)裁剪后拼成右边的长方形.
(1)请写出上述剪拼过程中所揭示的乘法公式;
(2)请运用乘法公式简便计算:20192﹣2020×2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一条笔直的公路进行跑步训练,可以用如图所示一条直线上来刻画他在公路上跑步情境.假定向右跑步的路程记为正数,向左跑步的路程记为负数,则所跑步的各段路程依次记为:+5,-3,-6,+8,-6,+12,-10.(单位:百米)
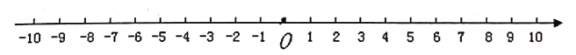
(1)小明最后是否回到出发点![]() ?
?
(2)小明在跑步过程中距离出发点![]() 最远是多少米?.
最远是多少米?.
(3)在跑步过程中,如果小明每跑1千米会消耗约60卡热量,那么小明此次训练一共会消耗多少卡?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并完成任务:
点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ;
;![]() 两点之间的距离表示为
两点之间的距离表示为![]() .
.
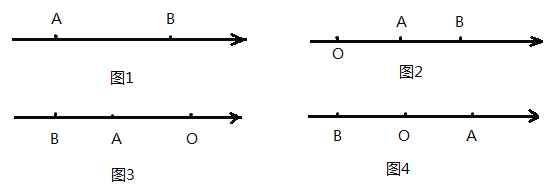
当![]() 两点中有一点在原点时,不妨设点
两点中有一点在原点时,不妨设点![]() 在原点,如图1所示,
在原点,如图1所示, ![]() ;
;
当![]() 两点都不在原点时,分三种情况,
两点都不在原点时,分三种情况,
情况一:如图2所示,点![]() 都在原点的右侧,
都在原点的右侧,![]() ;
;
情况二:如图3所示,点![]() 都在原点左侧,
都在原点左侧,![]() ;
;
情况三:如图4所示,点![]() 在原点的两边,
在原点的两边,![]() ;
;
综上所述,若点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,则数轴上
,则数轴上![]() 两点之间的距离为
两点之间的距离为![]() .
.
任务一:数轴上表示2和5的两点之间的距离是________,数轴上表示-2和-5的两点之间的距离是________,数轴上表示3和-1的两点之间的距离是________.
任务二:点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,那么
,那么![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离之和可表示为_________(用含绝对值的式子表示).如果
的距离之和可表示为_________(用含绝对值的式子表示).如果![]() ,那么
,那么![]() 为________.
为________.
任务三:当![]() 取最小值时,
取最小值时, ![]() =________,
=________, ![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )

A. 16B. 32C. 64D. 128
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,OB=4,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两条角平分线所在的直线相交于点F,则点A在运动过程中线段BF的最小值为( )
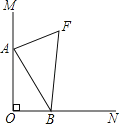
A. 4B. ![]() C. 8D. 2
C. 8D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我县新区部分小区位置简图.设港澳城为点A,水榭花都为点B,朝阳家园为点C,滨海华庭为点D,阳光家园为点E,盛世嘉苑为点F,设每个小格的单位为1.
(1)请建立适当的平面直角坐标系,并写出六个小区的坐标;
(2)依次连接点A、C、E、B,请求出四边形ACEB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com