
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E. 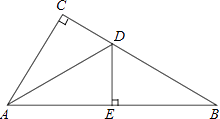
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.
【答案】
(1)证明:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中
![]()
∴Rt△ACD≌Rt△AED(HL)
(2)解:∵DC=DE=1,DE⊥AB,
∴∠DEB=90°,
∵∠B=30°,
∴BD=2DE=2
【解析】(1)根据角平分线性质求出CD=DE,根据HL定理求出另三角形全等即可;(2)求出∠DEB=90°,DE=1,根据含30度角的直角三角形性质求出即可.
【考点精析】根据题目的已知条件,利用角平分线的性质定理和含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,为了躲避台风,一轮船一直由西向东航行,上午10点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,中午12点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船是否能一直向东航行? 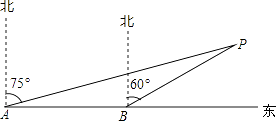
查看答案和解析>>
科目:初中数学 来源: 题型:
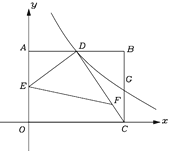
【题目】如图,平面直角坐标系中,矩形OABC的顶点B在第一象限,点C在x轴上,点A在y轴上,D、E分别是AB,OA中点.过点D的双曲线![]() 与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ).
与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ).
A. ![]() B.
B. ![]() C. 6 D. 10
C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
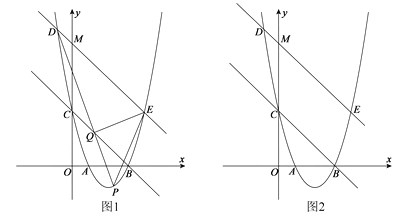
【题目】如图1,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 沿
沿![]() 轴向上平移4个单位长度后恰好经过
轴向上平移4个单位长度后恰好经过![]() 两点。
两点。
(1)求直线![]() 及抛物线的解析式;
及抛物线的解析式;
(2)将直线![]() 沿
沿![]() 轴向上平移5个单位长度后与抛物线交于
轴向上平移5个单位长度后与抛物线交于![]() 两点,若点
两点,若点![]() 是抛物线位于直线
是抛物线位于直线![]() 下方的一个动点,连接
下方的一个动点,连接![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() 和
和![]() 。设
。设![]() 的面积为
的面积为![]() ,当S取得最大值时,求出此时点
,当S取得最大值时,求出此时点![]() 的坐标及
的坐标及![]() 的最大值;
的最大值;
(3)如图2,记(2)问中直线![]() 与
与![]() 轴交于
轴交于![]() 点,现有一点
点,现有一点![]() 从
从![]() 点出发,先沿
点出发,先沿![]() 轴到达
轴到达![]() 点,再沿
点,再沿![]() 到达
到达![]() 点,已知
点,已知![]() 点在
点在![]() 轴上运动的速度是每秒2个单位长度,它在直线
轴上运动的速度是每秒2个单位长度,它在直线![]() 上运动速度是1个单位长度。现要使
上运动速度是1个单位长度。现要使![]() 点按照上述要求到达
点按照上述要求到达![]() 点所用的时间最短,请简述确定
点所用的时间最短,请简述确定![]() 点位置的过程,求出点
点位置的过程,求出点![]() 的坐标,不要求证明。
的坐标,不要求证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com