
分析 (1)8分钟进24吨,则每分钟进3吨,则当0≤t≤8时,Q=3t;由于进油管和出油管同时打开16分钟,油罐内的油从24吨增至40吨,每分钟进1吨,所以当8≤t≤24时,Q=t+16;由于出油管的速度为每分钟出油2吨,则40吨需20分钟,则24≤t≤44时,Q=-2t+88;
(2)利用描点法画出三个函数图象.
解答 解:(1)当0≤t≤8时,Q=$\frac{24}{8}$t=3t;
当8≤t≤24时,Q=24+$\frac{40-24}{16}$(t-8)=t+16;
当24≤t≤44时,Q=40-2(t-24)=-2t+88;
(2)如图,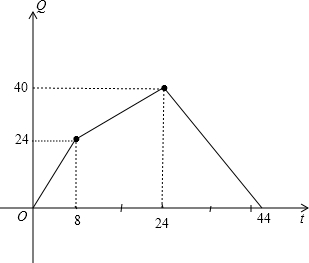
点评 本题考查了一次函数的应用:分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com