
【题目】“网络红包”是互联网运营商、商家通过组织互联网线上活动、派发红包的互联网工具,是朋友间互道祝福的表达形式之一.“网络红包”春节活动已经逐渐深入到大众的生活中,得到了人们较为广泛的关注.根据某咨询公司(2018年中国春节“网络红包”专题调查报告》显示:在接受调查的8万名网民中,对“网络红包”春节话动了解程度的占比方面,“较为了解”和“很了解”的网民共占比64%,分别占比36%和28%.在“不了解”和“只了解一两个“的受访网民中,“不了解”的网民人数比“只了解一两个”的网民人数多25%.如图是该咨询公司绘制的“中国网民关于‘网络红包’春节活动了解情况调查”统计图(不完整).
请根据以上信息解答下列问题:
(1)在受访的网民中,“不了解”和“只了解一两个”的网民人数共有 万人,其中“不了解”的网民人数是 万人;
(2)请将扇形统计图补充完整;
(3)2017除夕晚上小聪和爸爸、妈妈一起玩微信抢红包游戏,他们约定由爸爸在家人微信群中先后发两次“拼手气红包”,每次发放的红包数是3个,每个红包抽到的金额随机(每两个红包的金额都不相等),每次谁抽到红包的金额最大谁就是“手气最佳”者,求两次游戏中小聪都能获得“手气最佳”的概率为多少?

【答案】(1) 2.88,1.6;(2)见解析;(3)![]() .
.
【解析】分析:(1)①用8万ד不了解”和“只了解一两个”所对应的百分比求出“不了解”和“只了解一两个”的人数;②设“只了解一两个”的网民人数为x万人,则 “不了解”的网民人数为1.25x,
根据“只了解一两个”的网民人数+“不了解”的网民人数=2.88万人列方程求解;
(2)计算出“只了解一两个”的网民人数和 “不了解”的网民人数所占的百分比,然后补全统计图;
(3)先列出树状图,用符合条件的情况数除以所有情况数即可.
详解:(1)∵“不了解”和“只了解一两个”所对应的百分比为1﹣64%=36%,
∴“不了解”和“只了解一两个”的网民人数为8×36%=2.88万人,
设“只了解一两个”的网民人数为x万人,则 “不了解”的网民人数为1.25x,
则x+1.25x=2.88,
解得:x=1.28,
则1.25x=1.6,
即“不了解”的网民人数是1.6万人,
故答案为:2.88,1.6;
(2)“不了解”的网民人数占总人数的百分比为![]() ×100%=20%,
×100%=20%,
“只了解一两个”的网民人数占总人数的百分比为![]() ×100%=16%,
×100%=16%,
补全扇形图如下:

(3)设“手气最佳”的红包为A、其它两个红包为B、C,
画树状图如下:

由树状图可知,共有9种等可能结果,其中小聪两次抽到“手气最佳”的结果有1种,所以两次游戏中小聪都能获得“手气最佳”的概率为![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )

A. 10 B. 12 C. 15 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,A点坐标为(4,3),B点坐标为(-1,4),C点坐标为(-3,1).
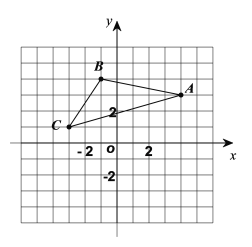
(1)在图中画出△ABC关于x轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标.
(2)在x轴上画出点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,



(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OPDE的值;
(3)如图3,已知点F坐标为(2,2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①mn为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你观察下列式子:
![]()
![]()
![]()
![]()
……
根据上面的规律,解答下列问题:
(1)当![]() 时,
时,
计算![]() …
…![]() =_________;
=_________;
(2)设![]() …
…![]() ,则a的个位数字为 ;
,则a的个位数字为 ;
(3)求式子![]() …
…![]() 的和.
的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 交y轴于点C,交x轴于点D,直线
交y轴于点C,交x轴于点D,直线![]() 经过点A(4,0),且两直线交于点B(2,m).
经过点A(4,0),且两直线交于点B(2,m).

(1)求m的值和直线![]() 的函数表达式;
的函数表达式;
(2)直线![]() 在第一象限内的部分有一点E,且
在第一象限内的部分有一点E,且![]() ,求出点E的坐标,并在y轴上找一点P,使得BP+PE的值最小,求出P的坐标和这个最小值;
,求出点E的坐标,并在y轴上找一点P,使得BP+PE的值最小,求出P的坐标和这个最小值;
(3)在(2)的条件下,若点Q为y轴上一点,且△BPQ为等腰三角形,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO,△A1B1C1,△A2B2C2,…都是正三角形,边长分别为2,22,23,…,且BO,B1C1,B2C2,…都在x轴上,点A,A1,A2,…从左至右依次排列在x轴上方,若点B1是BO中点,点B2是B1C1中点,…,且B为(﹣2,0),则点A6的坐标是( )

A. (61,32![]() ) B. (64,32
) B. (64,32![]() ) C. (125,64
) C. (125,64![]() ) D. (128,64
) D. (128,64![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com