
分析 ①直接利用利用已知条件才想得出答案;
②直接利用已知条件规律用n(n为正整数)表示的等式即可;
③利用发现的规律将原式变形得出答案.
解答 解:①猜想:$\sqrt{1+\frac{1}{{7}^{2}}+\frac{1}{{8}^{2}}}$=1+$\frac{1}{7}$-$\frac{1}{8}$=1$\frac{1}{56}$;
故答案为:1+$\frac{1}{7}$-$\frac{1}{8}$,1$\frac{1}{56}$;
②归纳:根据你的观察,猜想,写出一个用n(n为正整数)表示的等式:
$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{{n}^{2}+n+1}{{n}^{2}+n}$;
③应用:$\sqrt{\frac{82}{81}+\frac{1}{100}}$
=$\sqrt{1+\frac{1}{81}+\frac{1}{100}}$
=$\sqrt{1+\frac{1}{{9}^{2}}+\frac{1}{1{0}^{2}}}$
=1+$\frac{1}{9}$-$\frac{1}{10}$
=1$\frac{1}{90}$.
点评 此题主要考查了二次根式的性质与化简,正确发现数字变化规律是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 图象经过(1,-1) | B. | 图象位于二、四象限 | ||
| C. | 图象是中心对称图形 | D. | y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x-3<(4x+1)-1 | B. | 3(x-3)<2(2x+1)-1 | C. | 2(x-3)<3(2x+1)-6 | D. | 3x-9<4x-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1500m | B. | 4500m | C. | 3700m | D. | 5500m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=-6 | B. | a=5,b=6 | C. | a=1,b=6 | D. | a=5,b=-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个有理数不是正数就是负数 | |
| B. | 0是绝对值最小的实数 | |
| C. | 平方根等于本身的数是0和1 | |
| D. | 数轴上位于原点两侧的数互为相反数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
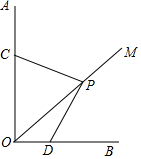 已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论.
已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com