
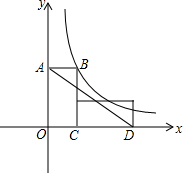
 ��ͼ����ƽ��ֱ������ϵ�У������Ϊ2�ij�����OABC���ҷ�ת90�㣬��B���ڵ�D������֪��B�ں���y=$\frac{k}{x}$��k��0����ͼ���ϣ�OA=2��
��ͼ����ƽ��ֱ������ϵ�У������Ϊ2�ij�����OABC���ҷ�ת90�㣬��B���ڵ�D������֪��B�ں���y=$\frac{k}{x}$��k��0����ͼ���ϣ�OA=2������ ��1�����ݳ�����OABC�����Ϊ2��OA=2���OC�ij�������ͼ����ת�����ʵó�D�����꼴�ɣ�
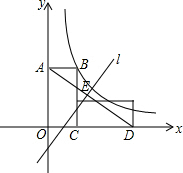
��2�����EΪ�߶�AD���е㣬����AD������ó�E�����꣬���ɵ�A��D����ֱ��l�Գƿ�ֱ֪��l���߶�AD�Ĵ�ֱƽ���ߣ����ô���ϵ�������ֱ��AD�Ľ���ʽ��ͬ���ɵó�ֱ��l�Ľ���ʽ��
��3����N��x��0����M��a��$\frac{2}{a}$�����ٷ�AMΪƽ���ı��εı���Խ�����������������ۣ�
���  �⣺��1���߳�����OABC�����Ϊ2��OA=2��
�⣺��1���߳�����OABC�����Ϊ2��OA=2��
��OC=1��
��B��1��2����
��k=1��2=2��
�߳�����OABC���ҷ�ת90�㣬��B���ڵ�D����
��CD=BC=2��
��D��3��0����
��2����ͼ1�����EΪ�߶�AD���е㣬
��A��0��2����D��3��0����
��E��$\frac{3}{2}$��1����
�ߵ�A��D����ֱ��l�Գƣ�
��ֱ��l���߶�AD�Ĵ�ֱƽ���ߣ�
��ֱ��AD�Ľ���ʽΪy=ax+b��a��0����
��$\left\{\begin{array}{l}b=2\\ 3a+b=0\end{array}\right.$�����$\left\{\begin{array}{l}a=-\frac{2}{3}\\ b=2\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=-$\frac{2}{3}$x+2��
��l��AD��
����ֱ��l�Ľ���ʽΪy=$\frac{3}{2}$x+c��
��$\frac{3}{2}$��$\frac{3}{2}$+c=1�����c=-$\frac{5}{4}$��
��ֱ��l�Ľ���ʽΪy=$\frac{3}{2}$x-$\frac{5}{4}$��
��3����ͼ2����N��x��0����M��a��$\frac{2}{a}$����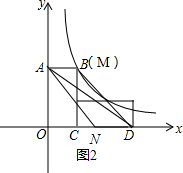
��AMΪƽ���ı��εı�ʱ��
��AM��DN��AB��DN��
���B���M�غϣ�
��AM=DN����B��1��2����D��3��0����
��N��2��0����M��1��2����
��AMΪƽ���ı��εĶԽ���ʱ��
��A��0��2����
��$\frac{a}{2}$=$\frac{3+x}{2}$��$\frac{\frac{2}{a}+3}{2}$=0�����a=0�������⣮
��N��2��0����
���� ���⿼����Ƿ����������ۺ��⣬�漰������������ͼ���ϵ�������ص㡢ƽ���ı��ε��ж������ʵ�֪ʶ���Ѷ����У�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��FG���ö˵������ĸ���߶εIJ������ʾ���������ֱ�ʾ��������3�֣�
��ͼ��FG���ö˵������ĸ���߶εIJ������ʾ���������ֱ�ʾ��������3�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
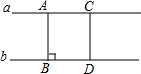 ��ͼ��ֱ��a��b��A��C��ֱ��a�ϵ����㣬B��D��ֱ��b�ϵ����㣬AB��b����ҪʹAB=CD��������һ������CD��b��
��ͼ��ֱ��a��b��A��C��ֱ��a�ϵ����㣬B��D��ֱ��b�ϵ����㣬AB��b����ҪʹAB=CD��������һ������CD��b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
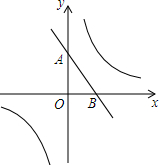 ֱ��y=-$\frac{4}{3}$x+8��x���ڵ�B����y���ڵ�A������ABO��ƽ���߽�y���ڵ�C�����߶�AC�Ƶ�A��ʱ����ת90����߶�AD����D��˫����y=$\frac{k}{x}$��k��0���ϣ�
ֱ��y=-$\frac{4}{3}$x+8��x���ڵ�B����y���ڵ�A������ABO��ƽ���߽�y���ڵ�C�����߶�AC�Ƶ�A��ʱ����ת90����߶�AD����D��˫����y=$\frac{k}{x}$��k��0���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com