
分析 ①只需比较tan60°与cos45°大小就可解决问题;
②由max{2x-5,3,7-4x}=3可得2x-5≤3且7-4x≤3,由此即可得到x的取值范围;
③不妨设a≤b≤c,由题可得c=$\frac{a+b+c}{3}$,则有a+b=2c,由a≤b≤c可得a+b≤2c,当且仅当a=b=c成立;
④可分三种情况(①2x-y+2最大,②-x+2y最大,③-x-y+1最大)讨论,即可解决问题.
解答 解:①∵tan60°=$\sqrt{3}$,cos45°=$\frac{\sqrt{2}}{2}$,
∴max{tan60°,cos45°}=$\sqrt{3}$,故①错误;
②∵max{2x-5,3,7-4x}=3,
∴$\left\{\begin{array}{l}{2x-5≤3}\\{7-4x≤3}\end{array}\right.$,
解得:1≤x≤4,故②正确;
③不妨设a≤b≤c,
∵max{a,b,c}=$\frac{a+b+c}{3}$,
∴c=$\frac{a+b+c}{3}$,
∴a+b=2c.
∵a≤b≤c,
∴a≤c,b≤c,
∴a+b≤2c,
当且仅当a=c且b=c时,a+b=2c,故③正确;
④当2x-y+2最大时,
∵max{2x-y+2,-x+2y,-x-y+1}=1,
∴$\left\{\begin{array}{l}{2x-y+2=1}\\{2x-y+2≥-x+2y}\\{2x-y+2≥-x-y+1}\end{array}\right.$,
即$\left\{\begin{array}{l}{y=2x+1}\\{3x-3y+2≥0}\\{x≥-\frac{1}{3}}\end{array}\right.$,
把y=2x+1代入3x-3y+2≥0,得x≤-$\frac{1}{3}$.
又∵x≥-$\frac{1}{3}$,
∴x=-$\frac{1}{3}$,
∴y=2×(-$\frac{1}{3}$)+1=$\frac{1}{3}$.
同理:当-x+2y最大时,x=-$\frac{1}{3}$,y=$\frac{1}{3}$;
当-x-y+1最大时,x=-$\frac{1}{3}$,y=$\frac{1}{3}$.
故④正确.
故答案为②③④.
点评 本题属于新定义型,主要考查了特殊角的三角函数值、解一元一次不等式组、不等式的性质等知识,运用不等式的性质是解决第③小题的关键,运用分类讨论的思想是解决第④小题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查你班同学的年龄情况 | B. | 为订购校服,了解学生衣服的尺寸 | ||
| C. | 考察一批炮弹的杀伤半径 | D. | 对航天飞机上的零部件进行检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
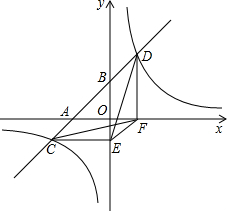 如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com