
分析 (1)直接根据题意售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件,进而得出等量关系;
(2)利用每件利润×销量=总利润,进而利用配方法求出即可;
(3)根据月利润不少于6000元即W≥6000可得不等式,结合二次函数图象解不等式可得x的范围,可得答案.
解答 解:(1)当x>0时,y=300-10x,当x<0时,y=300-20x;
故答案为:y=300-10x,y=300-20x.
(2)当x≥0时,W=(20+x)(300-10x)=-10x2+100x+6000=-10(x-5)2+6250,
∴当x=5时,W取得最大值,W最大值=6250元;
当x<0时,W=(20+x)(300-20x)=-20x2-100x+6000=-20(x+$\frac{5}{2}$)2+6125,
∴当x=-$\frac{5}{2}$时,W取得最大值,W最大值=6125元;
∵6250>6125,
∴当x=5时,W取得最大值,W最大值=6250元,
答:售价定为65元/盒时,才能使月利润w最大,月利润最大是6250元.
(3)当x≥0时,由W≥6000,可得:-10(x-5)2+6250≥6000,
解得:0≤x≤10,
当x<0时,由W≥6000,可得:-20(x+$\frac{5}{2}$)2+6125≥6000,
解得:-5≤x<0,
综上,-5≤x≤10,
答:故将销售价格控制在55元到70元之间(含55元和70元)才能使每月利润不少于6000元.
点评 此题主要考查了二次函数的应用以及配方法求二次函数最值等知识,熟练根据二次函数的解析式求其最值情况是解题的关键.


科目:初中数学 来源: 题型:解答题
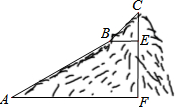 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
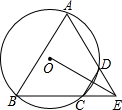 如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
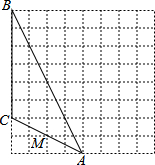 如图是一个由8×8个小正方形组成的方格纸,我们把顶点在正方形顶点的三角形称为格点三角形,图中的△ABC就是一个格点三角形,点M是AC的中点.
如图是一个由8×8个小正方形组成的方格纸,我们把顶点在正方形顶点的三角形称为格点三角形,图中的△ABC就是一个格点三角形,点M是AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
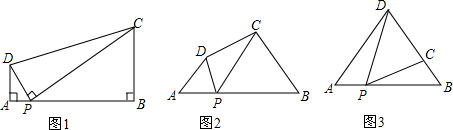
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,-3) | B. | (0,1) | C. | (0,3) | D. | (0,9) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com