
分析 (1)直接利用特殊角的三角函数值以及结合零指数幂的性质化简求出答案;
(2)直接利用特殊角的三角函数值以及结合零指数幂的性质、二次根式的性质化简求出答案.
解答 解:(1)原式=2×$\frac{\sqrt{2}}{2}$-4×($\frac{\sqrt{3}}{2}$)2-1+3×1
=$\sqrt{2}$-3-1+3
=$\sqrt{2}$-1;
(2)原式=-1-1+1-$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$+2=$\frac{1}{4}$.
点评 此题主要考查了特殊角的三角函数值以及零指数幂的性质、二次根式的性质等知识,正确化简各数是解题关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.
如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
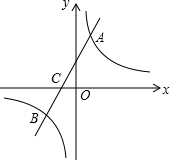 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
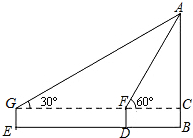 某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)
某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com