
����Ŀ��Ϊ��Ӧ���ҵġ�һ��һ·�����÷�չս�ԣ�����Ʒ����ʶ�������ʼ첿�Ŷ�A��B��C��D�ĸ�����������ͬ���ͺŵ������2000�����кϸ��ʼ�⣬ͨ�����ó�C���ҵĺϸ���Ϊ95%�������ݼ�����ݻ�������ͼ1��ͼ2������������ͳ��ͼ��
��1�����D���ҵ����Ϊ�� ����������ͳ��ͼ��D���Ҷ�Ӧ��Բ�Ľ�Ϊ�� ����
��2�����C���ҵĺϸ����Ϊ�� ����������ͼ1����������
��3��ͨ������˵���ϸ�������ǰ�����������������ң�
��4����Ҫ��A��B��C��D�ĸ������У������ȡ�������Ҳμӵ¹���ҵ��Ʒ�����ᣬ���á��б�����������ͼ���ķ��������3������������ͬʱ��ѡ�еĸ��ʣ�
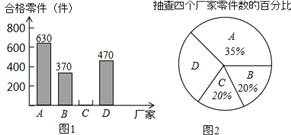
���𰸡���1��500�� 90�㣻��2��380����3���ϸ�������ǰ��������C��D�������ң���4��P��ѡ��C��D��=![]() ��
��
�������������������1�������D���������������D���������=��������ռ������D���Ҷ�Ӧ��Բ�Ľ�Ϊ360�����ռ������
��2��C���������=��������ռ������
��3������������ĺϸ��ʺ�һ���Ƚϵó��𰸼��ɣ�
��4��������״ͼ���оٳ����п��ܵĽ����Ȼ�����ø��ʹ�ʽ������⣮
�����������1��D�����������=1-20%-20%-35%=25%��
D���������=2000��25%=500����
D���Ҷ�Ӧ��Բ�Ľ�Ϊ360���25%=90����
��2��C���������=2000��20%=400����
C���ĺϸ������=400��95%=380����
��ͼ��

��3��A���Һϸ���=630����2000��35%��=90%��
B���Һϸ���=370����2000��20%��=92.5%��
C���Һϸ���=95%��
D���Һϸ���470��500=94%��
�ϸ�������ǰ��������C��D�������ң�
��4���������⻭����ͼ���£�
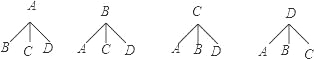
����12�������ѡ��C��D����2�֣�
��P��ѡ��C��D��=![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
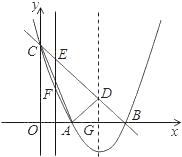
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=��![]() x2+
x2+![]() x+
x+![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D��
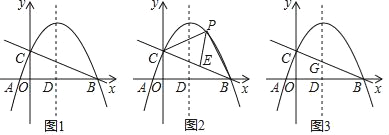
��1����ֱ��BC�Ľ���ʽ��
��2����ͼ2����PΪֱ��BC�Ϸ���������һ�㣬����PB��PC������PBC��������ʱ�����߶�BC����һ��E������B��C�غϣ���ʹPE+![]() BE��ֵ��С�����P�������PE+
BE��ֵ��С�����P�������PE+![]() BE����Сֵ��
BE����Сֵ��
��3����ͼ3����G���߶�CB���е㣬��������y=��![]() x2+
x2+![]() x+
x+![]() ��x��������ƽ�Ƶõ���������y�䣬y��������D��y���Ķ���ΪF����������y���ĶԳ����ϣ��Ƿ����һ��Q��ʹ����FGQΪֱ�������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��x��������ƽ�Ƶõ���������y�䣬y��������D��y���Ķ���ΪF����������y���ĶԳ����ϣ��Ƿ����һ��Q��ʹ����FGQΪֱ�������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ�������
A.ij�¼������ĸ���Ϊ![]() ������˵���������ظ��������У�����һ�η���
������˵���������ظ��������У�����һ�η���
B.һ������������100����С������8�Σ�ÿ�ζ�ֻ��������û�����������С���϶�����������ֻ�к���û�а���
C.����öһԪӲ��ͬʱ���£����ܳ��ֵ������У���1����ö��Ϊ������2����ö��Ϊ������3��һ��һ��������ͬʱ������öӲ�ң�����һ��һ���ĸ�����![]()
D.���꼶����400��ͬѧ��һ��������ͬһ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y1��mx2��nx��m+n��m��0����
��������֤���ú���ͼ����x����н��㣻
��������m��n��3��
����������m��x��1ʱ�����κ��������ֵС��0����m��ȡֵ��Χ��
��������A��p��q��Ϊ����y2��|mx2��nx��m+n|ͼ���ϵĶ��㣬����4��p����1ʱ����A��ֱ��y����x+4���Ϸ�����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѧ����������Ϊ50Ԫ�ġ��ִ�����ʵ䡷�����мס����������۴��飬�갴���·�����������ֻ��1������ԭ�����ۣ���һ���Թ������1������������30��ʱ��ÿ�һ�����ۼ��ڱ�۵Ļ������Ż�2%��������2����ÿ���ۼ��Ż�2%����������ÿ���ۼ��Ż�4%���Դ����ƣ���������30����ÿ���ۼ�20Ԫ�������һ�ɰ���۵�6�����ۣ�
��1���ֱ�д��������깺������ܼ�y����y���빺�鱾��x֮��ĺ�����ϵʽ��
��2������Щѧ��һ���Թ������30��ʱ����ôȥ�ļ���깺������㣬Ϊʲô����Ҫһ���Թ�����30��ʱ����д��y��y��y����y�����빺����x֮��ĺ���ʽ��������ͼ�������ú���ͼ�����ȥ�ļ���깺������㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������Ϊ��2����1����������y��ax2+bx+c��a��0����y�ύ�ڵ�C��0��3������x�ύ��A��B���㣮
��1���������ߵı���ʽ��
��2���������ߵĶԳ�����ֱ��BC���ڵ�D������AC��AD�����ACD�������
��3����EΪֱ��BC��һ���㣬����E��y���ƽ����EF���������߽��ڵ�F�����Ƿ���ڵ�E��ʹ����D��E��FΪ��������������BCO���ƣ������ڣ����E�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����·�����������Ƹ�AB��CD����С��վ�ڵ�N��ʱ���ڵ�C��������С����Ӱ������ΪNB���ڵ�A��������С����Ӱ��ΪNE�����BD=24m��NB=6m��NE=2m.
��1������������MN=1.6m����AB�ij���
��2�����ж��������Ƹ˵ĸ߶��Ƿ���ȣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μ�ij�����������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ���������С�������ᣬ����С������һ����������û���ã�ʹ����������������������ȥ������һ���һ������ѡ���
��1�����С����һ�ⲻʹ��������������ôС����Ե�һ����ĸ�����������
��2�����С���������������ڵڶ���ʹ�ã�������״ͼ�����б�������С��˳��ͨ�صĸ��ʣ�
��3���Ӹ��ʵĽǶȷ������㽨��С���ڵڼ���ʹ��������������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��ax2+bx+c��ͼ����x�ύ��A��2��0����B����8��0�����㣬��y�ύ�ڵ�C��0����8����
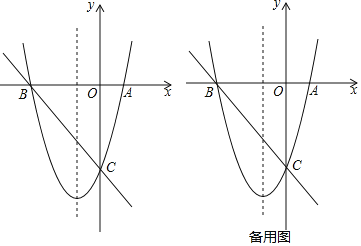
��1���������ߵĽ���ʽ��
��2����F��ֱ��BC�·��������ϵ�һ�㣬����BCF��������ʱ�������F�����ꣻ
��3���ڣ�2���������£��Ƿ���������ĵ�Q��0��m����ʹ�á�BFQΪ���������Σ�����У���ֱ��д����Q�����ꣻ���û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com