
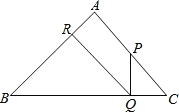
ЁОЬтФПЁПШчЭМЫљЪОЃЌе§ЗНаЮABCDжаЃЌЕуEЁЂFЁЂGЗжБ№ЪЧБпADЁЂABЁЂBCЕФжаЕуЃЌСЌНгEPЁЂFGЃЎ
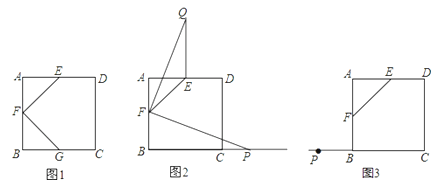
ЃЈ1ЃЉШчЭМ1ЃЌжБНгаДГіEFгыFGЕФЙиЯЕ____________ЃЛ
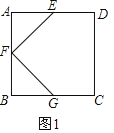
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуPЮЊBCбгГЄЯпЩЯвЛЖЏЕуЃЌСЌНгFPЃЌНЋЯпЖЮFPвдЕуFЮЊа§зЊжааФЃЌФцЪБеыа§зЊ90ЁуЃЌЕУЕНЯпЖЮFHЃЌСЌНгEHЃЎ
ЂйЧѓжЄЃКЁїFFEЁеЁїPFGЃЛЂкжБНгаДГіEFЁЂEHЁЂBPШ§епжЎМфЕФЙиЯЕЃЛ
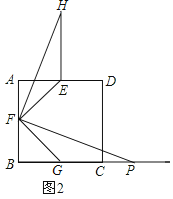
ЃЈ3ЃЉШчЭМ3ЃЌШєЕуPЮЊCBбгГЄЯпЩЯЕФвЛЖЏЕуЃЌСЌНгFPЃЌАДее(2)жаЕФзіЗЈЃЌдкЭМ(3)жаВЙШЋЭМаЮЃЌВЂжБНгаДГіEFЁЂEHЁЂBPШ§епжЎМфЕФЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉEFЁЭFGЃЌEF=FGЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉВЙШЋЭМаЮШчЭМ3ЫљЪОЃЌ![]() EF+BP=EHЃЎ
EF+BP=EHЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЯпЖЮжаЕуЕФЖЈвхЧѓГіAE=AF=BF=BGЃЌЕУГіЁЯAFE=ЁЯAEF=ЁЯBFG=ЁЯBGF=45ЁуЃЌЧѓГіЁЯEFGЕФЖШЪ§ЃЌгЩЁАSASЁБжЄЕУЁїAEFКЭЁїBFGШЋЕШЃЌЕУГіEF=FGЃЌМДПЩЕУГіНсЙћЃЛ
ЃЈ2ЃЉЂйгЩа§зЊЕФаджЪЕУГіЁЯPFH=90ЁуЃЌFP=FHЃЌжЄГіЁЯGFP=ЁЯEFHЃЌгЩSASМДПЩЕУГіЁїHFEЁеЁїPFGЃЛ
ЂкгЩШЋЕШШ§НЧаЮЕФаджЪЕУГіEH=PGЃЌгЩЕШбќжБНЧШ§НЧаЮЕФаджЪЕУГіEF=![]() AF=
AF=![]() BGЃЌвђДЫBG=
BGЃЌвђДЫBG=![]() EFЃЌдйгЩBG+GP=BPЃЌМДПЩЕУГіНсТлЃЛ
EFЃЌдйгЩBG+GP=BPЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉИљОнЬтвтзїГіЭМаЮЃЌШЛКѓЭЌЃЈ2ЃЉЕФЫМТЗЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЫљЪОЃК
ЁпЕуEЁЂFЁЂGЗжБ№ЪЧБпADЁЂABЁЂBCЕФжаЕуЃЌ
ЁрAE=AF=BF=BGЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯAFE=ЁЯAEF=ЁЯBFG=ЁЯBGF=45ЁуЃЌ
ЁрЁЯEFG=180Ёу-ЁЯAFE-ЁЯBFG=180Ёу-45Ёу-45Ёу=90ЁуЃЌ
ЁрEFЁЭFGЃЌ
дкЁїAEFКЭЁїBFGжаЃЌ
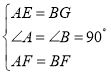 ЃЌ
ЃЌ
ЁрЁїAEFЁеЁїBFGЃЈSASЃЉЃЌ
ЁрEF=FGЃЌ
ЙЪД№АИЮЊЃКEFЁЭFGЃЌEF=FGЃЛ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃК
ЂйжЄУїЃКгЩЃЈ1ЃЉЕУЃКЁЯEFG=90ЁуЃЌEF=FGЃЌ
ЁпНЋЯпЖЮFPвдЕуFЮЊа§зЊжааФЃЌФцЪБеыа§зЊ90ЁуЃЌЕУЕНЯпЖЮFHЃЌ
ЁрЁЯPFH=90ЁуЃЌFP=FHЃЌ
ЁпЁЯGFP+ЁЯPFE=90ЁуЃЌЁЯPFE+ЁЯEFH=90ЁуЃЌ
ЁрЁЯGFP=ЁЯEFHЃЌ
дкЁїHFEКЭЁїPFGжаЃЌ
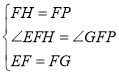 ЃЌ
ЃЌ
ЁрЁїHFEЁеЁїPFGЃЈSASЃЉЃЛ
ЂкНтЃКгЩЂйЕУЃКЁїHFEЁеЁїPFGЃЌЁрEH=PGЃЌ
ЁпAE=AF=BF=BGЃЌЁЯA=ЁЯB=90ЁуЃЌ
ЁрEF=![]() AF=
AF=![]() BGЃЌ
BGЃЌ
ЁрBG=![]() EFЃЌ
EFЃЌ
ЁпBG+GP=BPЃЌ
Ёр![]() EF+EH=BPЃЛ
EF+EH=BPЃЛ
ЃЈ3ЃЉНтЃКВЙШЋЭМаЮШчЭМ3ЫљЪОЃЌ![]() EF+BP=EHЃЎРэгЩШчЯТЃК
EF+BP=EHЃЎРэгЩШчЯТЃК
гЩЃЈ1ЃЉЕУЃКЁЯEFG=90ЁуЃЌEF=FGЃЌ
ЁпНЋЯпЖЮFPвдЕуFЮЊа§зЊжааФЃЌФцЪБеыа§зЊ90ЁуЃЌЕУЕНЯпЖЮFHЃЌ
ЁрЁЯPFH=90ЁуЃЌFP=FHЃЌ
ЁпЁЯEFG+ЁЯGFH=ЁЯEFHЃЌЁЯPFH+ЁЯGFH=GFPЃЌ
ЁрЁЯGFP=ЁЯEFHЃЌ
дкЁїHFEКЭЁїPFGжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїHFEЁеЁїPFGЃЈSASЃЉЃЌ
ЁрEH=PGЃЌ
ЁпAE=AF=BF=BGЃЌЁЯA=ЁЯABC=90ЁуЃЌ
ЁрEF=![]() AF=
AF=![]() BGЃЌ
BGЃЌ
ЁрBG=![]() EFЃЌ
EFЃЌ
ЁпBG+BP=PGЃЌ
Ёр![]() EF+BP=EHЃЎ
EF+BP=EHЃЎ


 бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
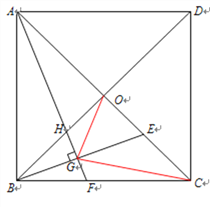
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌEЮЊOCЩЯЖЏЕу(гыЕуOВЛжиКЯ)ЃЌзїAFЁЭBEЃЌДЙзуЮЊGЃЌНЛBCгкFЃЌНЛB0гкHЃЌСЌНгOGЃЌCCЃЎ
(1)ЧѓжЄЃКAH=BEЃЛ
(2)ЪдЬНОПЃКЁЯAGOЕФЖШЪ§ЪЧЗёЮЊЖЈжЕ?ЧыЫЕУїРэгЩЃЛ
(3)ШєOGЁЭCGЃЌBG=![]() ЃЌЧѓЁїOGCЕФУцЛ§ЃЎ
ЃЌЧѓЁїOGCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєбљБОx1+1ЃЌx2+1ЃЌЁЃЌxn+1ЕФЦНОљЪ§ЮЊ10ЃЌЗНВюЮЊ2ЃЌдђЖдгкбљБОx1+2ЃЌx2+2ЃЌЁЃЌxn+2ЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
A. ЦНОљЪ§ЮЊ10ЃЌЗНВюЮЊ2 B. ЦНОљЪ§ЮЊ11ЃЌЗНВюЮЊ3
C. ЦНОљЪ§ЮЊ11ЃЌЗНВюЮЊ2 D. ЦНОљЪ§ЮЊ12ЃЌЗНВюЮЊ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊРЉДѓФкашЃЌЙњЮёдКОіЖЈдкШЋЙњЪЕЪЉЁАМвЕчЯТЯчЁБеўВп. ЕквЛХњСаШыМвЕчЯТЯчЕФВњЦЗЮЊВЪЕчЁЂБљЯфЁЂЯДвТЛњКЭЪжЛњЫФжжВњЦЗ. ФГЯивЛМвМвЕчЩЬГЁЃЌШЅФъЕквЛМОЖШЖдвдЩЯЫФжжВњЦЗЕФЯњЪлЧщПіНјааСЫЭГМЦЃЌЛцжЦСЫШчЯТЕФЭГМЦЭМЃЌЧыФуИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉИУЩЬГЁЕквЛМОЖШвЛЙВЯњЪлСЫ_________ЬЈМвЕчЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЌВЂЧѓГіЩШаЮЭГМЦЭМжаВЪЕчЫљдкЕФЩШаЮдВаФНЧЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгавЛИіБпГЄЮЊ![]() ЕФДѓе§ЗНаЮКЭСНИіБпГЄЮЊbЕФаЁе§ЗНаЮЃЌЗжБ№НЋЫћУЧАДееЭМЂйКЭЭМЂкЕФаЮЪНАкЗХЃЌ
ЕФДѓе§ЗНаЮКЭСНИіБпГЄЮЊbЕФаЁе§ЗНаЮЃЌЗжБ№НЋЫћУЧАДееЭМЂйКЭЭМЂкЕФаЮЪНАкЗХЃЌ

ЃЈ1ЃЉгУКЌга![]() ЕФДњЪ§ЪНЗжБ№БэЪОвѕгАУцЛ§ЃК
ЕФДњЪ§ЪНЗжБ№БэЪОвѕгАУцЛ§ЃК![]() ,
,![]() ЃЌ
ЃЌ![]() .
.
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓГіЭМЂлжаЕФвѕгАВПЗжУцЛ§.
ЃЌЧѓГіЭМЂлжаЕФвѕгАВПЗжУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРЯЪІдкКкАхЩЯЪщаДСЫвЛИіе§ШЗЕФбнЫуЙ§ГЬЃЌЫцКѓгУЪжеЦЮцзЁСЫвЛИіЖрЯюЪНЃЌаЮЪНШчЯТЃК![]() +ЃЈЉ3x2+5xЉ7ЃЉ=Љ2x2+3xЉ6
+ЃЈЉ3x2+5xЉ7ЃЉ=Љ2x2+3xЉ6
ЃЈ1ЃЉЧѓЫљЮцЕФЖрЯюЪНЃЛ
ЃЈ2ЃЉШєxЪЧ![]() x=Љ
x=Љ![]() x+3ЕФНтЃЌЧѓЫљЮцЖрЯюЪНЕФжЕЃЛ
x+3ЕФНтЃЌЧѓЫљЮцЖрЯюЪНЕФжЕЃЛ
ЃЈ3ЃЉШєxЮЊе§ећЪ§ЃЌxУПШЁвЛИіжЕЃЌЖМПЩвдЧѓГіЫљЮцЖрЯюЪНЕФжЕЃЌЧыФуШЮШЁxЕФМИИіжЕЃЈВЛвЊаДдкД№ЬтжНЩЯЃЉЃЌЗЂЯжЫќУЧжЎМфгавЛЖЈЕФЙцТЩЃЌЧыгУКЌxЕФЪНзгБэЪОетвЛНсТлЃК____________=_____________ЃЛ
ЃЈ4ЃЉШєЫљЮцЖрЯюЪНЕФжЕЮЊ729ЃЌЧыжБНгаДГіxЕФШЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгк
ЕФЭМЯѓНЛгк![]() )СНЕугыxжсЃЌyжсЗжБ№НЛгкAЁЂB(0ЃЌ2)СНЕуЃЌШчЙћ
)СНЕугыxжсЃЌyжсЗжБ№НЛгкAЁЂB(0ЃЌ2)СНЕуЃЌШчЙћ![]() ЕФУцЛ§ЮЊ6.
ЕФУцЛ§ЮЊ6.

(1)ЧѓЕуAЕФзјБъ;
(2)ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪН;
(3)ШчЭМ2ЃЌСЌНгDOВЂбгГЄНЛЗДБШР§КЏЪ§ЕФЭМЯѓгкЕуEЃЌСЌНгCEЃЌЧѓЕуEЕФзјБъКЭ![]() ЕФУцЛ§
ЕФУцЛ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКдкЁїABCжаЃЌЁЯA=90ЁуЃЌAB=AC=1ЃЌPЪЧACЩЯВЛгыAЁЂCжиКЯЕФвЛЖЏЕуЃЌPQЁЭBCгкQЃЌQRЁЭABгкRЃЎ
ЃЈ1ЃЉЧѓжЄЃКPQ=CQЃЛ
ЃЈ2ЃЉЩшCPЕФГЄЮЊxЃЌQRЕФГЄЮЊyЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНМАздБфСПxЕФШЁжЕЗЖЮЇЃЌВЂдкЦНУцжБНЧзјБъЯЕзїГіКЏЪ§ЭМЯѓЃЎ
ЃЈ3ЃЉPRФмЗёЦНаагкBCЃПШчЙћФмЃЌЪдЧѓГіxЕФжЕЃЛШєВЛФмЃЌЧыМђЪіРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГізтГЕЫОЛњФГЬьЩЯЮчШЋЪЧдкЖЋЮїзпЯђЕФТЗЩЯдЫгЊЃЌШчЙћЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЫћетЬьааГЕРяГЬЃЈЕЅЮЛЃКЧЇУзЃЉШчЯТЃК
-9ЃЌ+5ЃЌ-7ЃЌ+10ЃЌ+5ЃЌ-8ЃЌ-4ЃЌ+6ЃЌ-5ЃЌ-4
ЃЈ1ЃЉНЋзюКѓвЛУћГЫПЭЫЭДяЪБЃЌЫћОрГіЗЂЕиЖрдЖЃПдкГіЗЂЕиЪВУДЗНЯђЃП
ЃЈ2ЃЉШчЙћУПааЪЛ1ЧЇУзКФгЭ0.4Щ§ЃЌУПЩ§гЭ7дЊЃЌЫћвЛЩЯЮчЕФЯћКФЕФгЭЛЈЗбЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com