
【题目】某商场二楼摆出一台游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物,等可能地向左或向右边落下.
(1)若乐乐投入一个小球,则小球落入B区域的概率为 .
(2)若乐乐先后投两个小球,求两个小球同时落在A区域的概率.
【答案】
(1)![]()
(2)解:先后共投2个小球,可能会出现的结果列树状图如下:
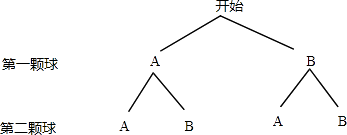
由树状图可知,共有4种等可能情况,其中2个小球均落在A区只有1种情况,
则2个小球均落在A区的概率为 ![]()
【解析】解:(1)∵乐乐投入一个小球,
∴小球落入B区域的概率为 ![]() ;
;
所以答案是: ![]() ;
;
【考点精析】认真审题,首先需要了解列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率),还要掌握概率公式(一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元.
(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任拿出200元学校奖励基金交给小芳,再次购买上述价格的钢笔和笔记本共48件作为奖品,奖励给校运动会中表现突出的同学,经双方协商,商店给出优惠是购买商品的总金额超出50的部分给打九折,请问小芳至少要买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图1,先把正方形ABCD对折,折痕为MN.
第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.
(1)判断△PBC的形状,并说明理由;
(2)作点C关于直线AP的对称点C′,连接PC′、DC′.
①在图2中补全图形,并求出∠APC′的度数;
②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个七边形棋盘如图所示,7个顶点顺序从0到6编号,称为七个格子.一枚棋子放在0格,现在依逆时针移动这枚棋子,第一次移动1格,第二次移动2格,…,第n次移动n格.则不停留棋子的格子的编号有_____.
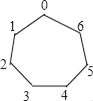
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1 , 给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③ ![]() 的值为定值;④当B1C=
的值为定值;④当B1C= ![]() DC时,AM=
DC时,AM= ![]() ,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上)
,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米. 
(1)则∠AOC=°(直接写出答案)
(2)求旗杆AB的高度(精确到0.1米,参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段![]() 是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若
是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若![]() 的坐标为(3,4).
的坐标为(3,4).
(1)![]() 的坐标为 ;
的坐标为 ;
(2)若线段AB上一点P的坐标为(![]() ,
,![]() ),则点P的对应点
),则点P的对应点![]() 的坐标 .
的坐标 .
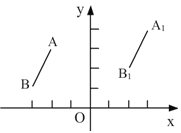
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“*”所代表的数是( )
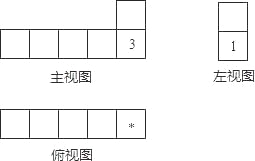
A. 2 B. 4 C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com