
【题目】已知等腰△ABC中,AB=AC,D是BC边上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是 .
【答案】36°或45°.
【解析】
试题分析:△ACD和△ABD都是等腰三角形,但没有说具体的边相等,所以应分情况讨论.
(1)AD=BD,DC=AD,那么△ADB和△ADC是全等三角形,可求得∠ADC=90°,那么∠C=45°;
(2)AB=BD,CD=AD,那么∠B=∠C=∠DAC,∠BAD=∠BDA=2∠C,然后用∠C表示出△ABC的内角和,即可求得5∠C=180°,那么∠C=36°.
解:应分两种情况:
(1)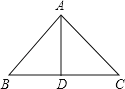
AD=BD,DC=AD,那么△ADB和△ADC是全等三角形,可求得∠ADC=90°,那么∠C=45°;
(2)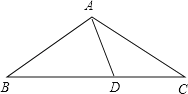
AB=BD,CD=AD,那么∠B=∠C=∠DAC,∠BAD=∠BDA=2∠C,然后用∠C表示出△ABC的内角和,即可求得5∠C=180°,那么∠C=36°.
故填36°或45°.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
①﹣10+8
②﹣20+(﹣14)﹣(﹣18)﹣13
③2﹣2÷(﹣![]() )×3
)×3
④﹣14﹣![]() ×[3﹣(﹣3)2]
×[3﹣(﹣3)2]
⑤﹣24×(﹣![]() +
+![]() ﹣
﹣![]() )
)
⑥﹣22+3×(﹣2)﹣(﹣4)2÷(﹣8)﹣(﹣1)100.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)线段AB的长度为 个单位长度,点M表示的数为 .
(2)当点Q运动到点M时,点P运动到点N,则MN的长度为 个单位长度.
(3)设点P运动的时间为t秒.是否存在这样的t,使PA+QA为5个单位长度?如果存在,请求出t的值和此时点P表示的数;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.
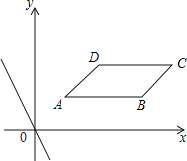
(1)k= ;
(2)若直线l过点D,求直线l的解析式;
(3)若直线l同时与边AB和CD都相交,求b的取值范围;
(4)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com