
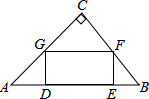
 如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6.
如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6.分析 (1)先由面积求出CH,再证明△GFC∽△ABC,得出比例式,由GF=DG求出DG的长;
(2)由△ADG≌△GCF时,DG=CF,AD=CG,AG=GF,再由△FEB∽△ACB得出比例式求出DG的长;
(3)由题意推出不成立.
解答 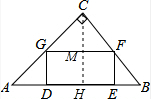 解:(1)过C作CH⊥AB于H,交GF于M,如图所示:
解:(1)过C作CH⊥AB于H,交GF于M,如图所示:
设DG=x,
∵四边形DEFG为正方形,
∴GF=DG=x,
∵∠C=90°,在Rt△ABC中,根据勾股定理得:
AB=$\sqrt{{6}^{2}{+8}^{2}}$=10,
∵S△ABC=$\frac{1}{2}$AB•CH=$\frac{1}{2}$AC•BC,
∴CH=$\frac{AC•BC}{AB}$=$\frac{6×8}{10}$,
∵GF∥DE,∴△GFC∽△ABC,
∴$\frac{CM}{CH}$=$\frac{GF}{AB}$,即$\frac{\frac{24}{5}-x}{\frac{24}{5}}$=$\frac{x}{10}$,
解得 x=$\frac{120}{37}$,即DG=$\frac{120}{37}$;
(2)能;当△BEF≌△GCF时,EF=CG,BE=CF,BF=GF,设EF=CG=y,
则AG=8-y;
∵∠ADG=∠C=90°,∠A=∠A,
∴△ADG∽△ACB中,
∴$\frac{DG}{AG}$=$\frac{BC}{AB}$,∴$\frac{y}{8-y}$=$\frac{3}{5}$,
解得 y=3,
即EF=3;
(3)不能,
∵DG=EF,∠ADG=∠BEF=90°,∠A=∠BFE,∠AGD=∠FBE
虽有四组条件,但不对应,要使△ADG与△BEF全等,
须使AD=EF,则AD=DG,即须使∠A=45°,
由AC=4,BC=3知,∠A不可能等于45°,
∴△ADG与△BEF不可能全等.
点评 本题考查了正方形的性质、相似三角形的判定与性质以及全等三角形的判定;证明三角形相似得出比例式是解决问题的关键.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
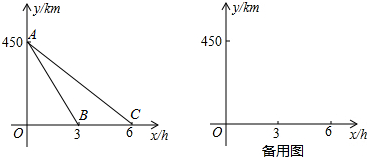
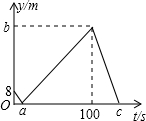 甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )
甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,$\sqrt{3}$≈1.73)
某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,-3)或(-5,-3) | B. | (-3,5)或(-3,-5) | C. | (-3,5) | D. | (-3,-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com