
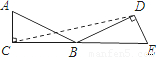
 如图,把一个直角三角形ABC绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时∠BDC的度数是
如图,把一个直角三角形ABC绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时∠BDC的度数是科目:初中数学 来源: 题型:
 如图,把一个直角三角形ABC绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时∠BDC的度数是( )
如图,把一个直角三角形ABC绕着30°角的顶点B顺时针旋转,使点A与CB的延长线上的点E重合,这时∠BDC的度数是( )| A、10° | B、15° | C、20° | D、30° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•大庆)如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(2013•大庆)如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.查看答案和解析>>
科目:初中数学 来源:2015届江苏连云港岗埠中学八年级9月月考模拟数学试卷(解析版) 题型:解答题
如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:解答题
如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年四川省遂宁市大英县九年级(上)期中数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com