
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
分析 (1)利用A型、B型、C型三款手机共60部,由A、B型手机的部数可表示出C型手机的部数;
(2)根据购机款列出等式可表示出x、y之间的关系;
(3)①由预估利润P=预售总额-购机款-各种费用,列出等式即可;
②根据题意列出不等式组,求出购买方案的种数,预估利润最大值即为合理的方案
解答 解:(1)根据题意,知购进C型手机的部数为60-x-y;
(2)根据题意,得:900x+1200y+1100(60-x-y)=61000,
整理,得:y=2x-50;
(3)①由题意,得:P=1200x+1600y+1300(60-x-y)-61000-1500=500x+500.
②购进C型手机部数为60-x-y=110-3x,根据题意,可列不等式组:
$\left\{\begin{array}{l}{x≥8}\\{2x-50≥8}\\{110-3x≥8}\end{array}\right.$,
解得:29≤x≤34,
∵P是x的一次函数,k=500>0,
∴P随x的增大而增大,
∴当x=34时,P取得最大值,最大值为17500元,
此时购进A型手机34部、B型手机18部、C型手机8部.
点评 此题考查了一次函数应用问题,解题的关键是结合图表,理解题意,求得一次函数解析式,然后根据函数的性质求解,注意函数思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
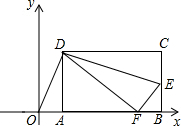 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
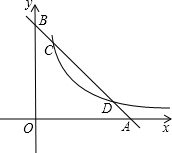 已知:一次函数y=-x+b的图象与x轴、y轴的交点分别为A、B与反比例函数$y=\frac{5}{x}(x>0)$的图象交于点C、D,且$\frac{BD}{BA}=\frac{2}{3}$.
已知:一次函数y=-x+b的图象与x轴、y轴的交点分别为A、B与反比例函数$y=\frac{5}{x}(x>0)$的图象交于点C、D,且$\frac{BD}{BA}=\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
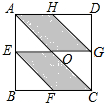 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
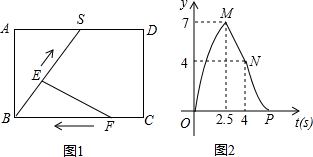
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
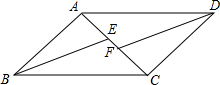 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.
如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com