
【题目】如图1,DEF分别为△ABC边ACABBC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是( )
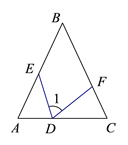
A. AE=FC B. AE=DE C. AE+FC=AC D. AD+FC=AB
科目:初中数学 来源: 题型:
【题目】把下面各数填入相应的大括号内.
-13.5,5,0,-10,-15%,![]()
负数集合:{ …},
非负数集合:{ …},
整数集合:{ …},
负分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a、b、c满足a=-b,|a+1|+(c-4)2=0,请回答问题:
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,P为数轴上一动点,其对应的数为x,若点P在线段BC上时,请化简式子:|x+1|-|1-x|+2|x-4|(请写出化简过程);
![]()
(3)若点P从A点出发,以每秒2个单位长度的速度向右运动,试探究当点P运动多少秒时,PC=3PB?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】厉害了,我的国!2018年10月24日,珠港澳大桥建成通车,成了世界瞩目的焦点.这座连接中国珠海、香港、澳门三座城市,全长55公里,投资1269亿元经过6年筹备与9年建设的跨海大桥,创造了400多项专利和七项世界之最,被誉为世界的第七大奇迹,是中国科技实力的伟大展现,令全球华人倍感骄傲与自豪.用科学记数法表示大桥的投资款正确的是( )
A.12.69×![]() 亿元B.1.269×
亿元B.1.269×![]() 元
元
C.1.269×![]() 元D.1.269×
元D.1.269×![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,
定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算.例如,2⊙5=2(2+5)﹣1=13.
(Ⅰ)求[1⊙(﹣2)]⊙3![]() 的值;
的值;
(Ⅱ)对于任意有理教m,n请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n=_____.(用含m,n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=﹣x+4于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.

(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
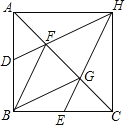
【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com