
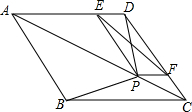
 如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF.
如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF.分析 (1)根据菱形的性质得出∠DAP=∠PAB,AD=AB,再利用全等三角形的判定得出△ABP≌△ADP即可;
(2)先证明四边形EPFD是平行四边形,再由全等三角形的性质得出BP=DP,由已知证出DP=EF,即可得出结论.
解答 (1)证明:∵点P是菱形ABCD对角线AC上的一点,
∴∠DAP=∠PAB,AD=AB,
∵在△APB和△APD中,$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠PAB=∠PAD}&{\;}\\{AP=AP}&{\;}\end{array}\right.$,
∴△ABP≌△ADP(SAS);
(2)证明:∵PE∥CD,PF∥AD,
∴四边形EPFD是平行四边形,
由(1)得:△ABP≌△ADP,
∴BP=DP,
又∵BP=EF,
∴DP=EF,
∴四边形EPFD是矩形.
点评 本题考查了矩形的判定、菱形的性质、全等三角形的判定与性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 市交委发布消息称,重庆三环高速铜梁至永川段已于2015年9月28日15时正式通车,从铜梁开车至永川车程将由目前的90分钟缩短到40多分钟. 铜永高速公路是我市“三环”高速公路的一段,设计双向四车道.项目起于铜梁区以北,与铜(梁)合(川)高速相接,止于永川区双石镇,与永(川)江(津)高速相接,设计时速80公里.项目全长64公里、总投资约39亿元,沿线设互通10处.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方50m处,过了4.8s后,测得小汽车与车速检测仪间距离为130m,这辆小汽车超速了吗?
市交委发布消息称,重庆三环高速铜梁至永川段已于2015年9月28日15时正式通车,从铜梁开车至永川车程将由目前的90分钟缩短到40多分钟. 铜永高速公路是我市“三环”高速公路的一段,设计双向四车道.项目起于铜梁区以北,与铜(梁)合(川)高速相接,止于永川区双石镇,与永(川)江(津)高速相接,设计时速80公里.项目全长64公里、总投资约39亿元,沿线设互通10处.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方50m处,过了4.8s后,测得小汽车与车速检测仪间距离为130m,这辆小汽车超速了吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com