
 时,试说明点G为线段EF的中点;
时,试说明点G为线段EF的中点; ,FC=
,FC= ,用含有
,用含有 的代数式来表示
的代数式来表示 ,并写出
,并写出 的取值范围
的取值范围 ,如图2,当
,如图2,当 时,讨论△
时,讨论△ 与△
与△ 是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.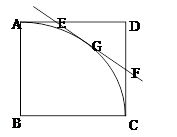

 (0<x<1).
(0<x<1). 时,由(2)得EF=EG+FG=AE+FC,
时,由(2)得EF=EG+FG=AE+FC, =
=  ,
, 或x2=
或x2= .
. 时,△AD1D∽△ED1F,
时,△AD1D∽△ED1F, ,AD=1,
,AD=1, 时,△ED1F与△AD1D不相似.
时,△ED1F与△AD1D不相似.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题





查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
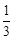 ,求tan ∠EBC的值.
,求tan ∠EBC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com