
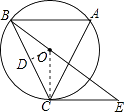
【题目】如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E. 
(1)求∠BCE的度数;
(2)若⊙O半径为3,求BE长.
【答案】
(1)解:连接OC,∵∠A=60°,∴∠BOC=120°,
又∵OB=OC,∴∠OCB=∠OBC=30°,
∵EC切⊙O于E,∴∠OCE=90°,
∴∠ECB=120°
(2)解:过点O作OD⊥BC于点D,
∵∠A=60°,
∴∠BOC=120°,
又∵∠CBE=∠BOC,
∴△BOC∽△BCE,
∴ ![]() =
= ![]()
∴BC2=BOBE;
∵BO=3,∠OBD=30°,
∴BD=BOcos30°= ![]() ,
,
∴BC=3 ![]() ,
,
∴(3 ![]() )2=3BE,
)2=3BE,
∴BE=9.
【解析】(1)利用切线的性质结合等腰三角形的性质得出∠OCE=90°,∠OCB=∠OBC=30°,进而求出∠BCE的度数;(2)利用相似三角形的判定与性质得出△BOC∽△BCE,进而得出 ![]() =
= ![]() ,进而得出答案.
,进而得出答案.
【考点精析】通过灵活运用切线的性质定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
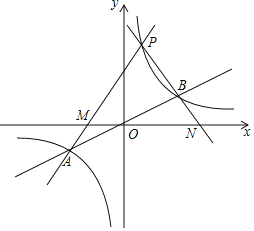
【题目】如图,函数![]() 与
与![]() 图象的交于点A,
图象的交于点A,![]() 若点A的坐标为
若点A的坐标为![]() .
.
![]() 点B的坐标为______;
点B的坐标为______;
![]() 若点P为第一象限内双曲线上不同于点B的任意一点.
若点P为第一象限内双曲线上不同于点B的任意一点.
![]() 设直线PA交x轴于点M,直线PB交x轴于点N,求证
设直线PA交x轴于点M,直线PB交x轴于点N,求证![]() ;
;
![]() 当P的坐标为
当P的坐标为![]() 时,连结PO延长交
时,连结PO延长交![]() 于C,求证四边形PACB为矩形.
于C,求证四边形PACB为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 ![]() ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.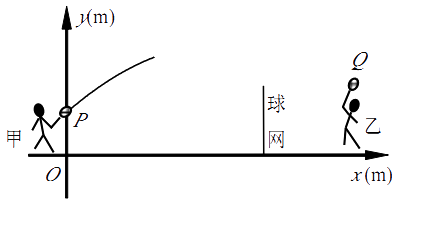
(1)当a= ![]() 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角). 
(1)若∠P2P3B=45°,CP1=;
(2)若 ![]() <BP3<
<BP3< ![]() ,则P1C长的取值范围是 .
,则P1C长的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
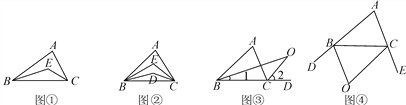
【题目】【问题】如图①,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=__ __;若∠A=n°,则∠BEC=__ _.
【探究】
(1)如图②,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB.若∠A=n°,则∠BEC=____;
(2)如图③,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图④,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要利用28米长的篱笆和一堵最大可利用长为12米的墙围成一个如图1的一边靠墙的矩形养鸡场,在围建的过程中遇到了以下问题,请你帮忙来解决.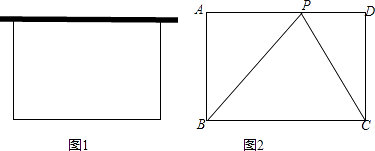
(1)这个矩形养鸡场要怎样建面积能最大?求出这个矩形的长与宽;
(2)在(1)的前提条件下,要在墙上选一个点P,用不可伸缩的绳子分别连接BP,CP,点P取在何处所用绳子长最短?
(3)仍然是矩形养鸡场面积最大的情况下,若把(2)中的不可伸缩的绳子改为可以伸缩且有弹性的绳子,点P可以在墙上自由滑动,求sin∠BPC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边![]() 的边长为2,现将等边
的边长为2,现将等边![]() 放置在平面直角坐标系中,点B和原点重合,点C在x轴正方向上,直线交x轴于点D,交y轴于点E,且
放置在平面直角坐标系中,点B和原点重合,点C在x轴正方向上,直线交x轴于点D,交y轴于点E,且![]() 如图
如图![]() ,现将等边
,现将等边![]() 从图1的位置沿x轴正方向以每秒1个单位长度的速度移动,边AB、AC分别与线段DE交于点G、
从图1的位置沿x轴正方向以每秒1个单位长度的速度移动,边AB、AC分别与线段DE交于点G、![]() 如图
如图![]() ,同时点P从
,同时点P从![]() 的顶点B出发,以每秒2个单位长度的速度沿折线
的顶点B出发,以每秒2个单位长度的速度沿折线![]() 运动
运动![]() 当点P运动到C时即停止活动,
当点P运动到C时即停止活动,![]() 也随之停止移动,设
也随之停止移动,设![]() 平移的时间为
平移的时间为![]() .
.
![]() 试求直线DE的解析式;
试求直线DE的解析式;
![]() 当点P在线段AC上运动时,设点P与点H的距离为y,求y与t的函数关系式,并写出定义域;
当点P在线段AC上运动时,设点P与点H的距离为y,求y与t的函数关系式,并写出定义域;
![]() 当点P在线段AB上运动时,
当点P在线段AB上运动时,![]() 中恰好有一个角的度数为
中恰好有一个角的度数为![]() ,请直接写出t的值,不必写过程.
,请直接写出t的值,不必写过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com