
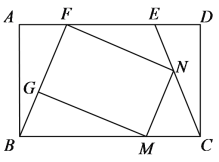
【题目】如图,在矩形ABCD中,点E、F在边AD上,AF=DE,连接BF、CE.
(1)求证:∠CBF=∠BCE;
(2)若点G、M、N在线段BF、BC、CE上,且 FG=MN=CN.求证:MG=NF;
(3)在(2)的条件下,当∠MNC=2∠BMG时,四边形FGMN是什么图形,证明你的结论.
【答案】(1)见解析;(2)见解析;(3)四边形FGMN是矩形,见解析
【解析】
(1)由“SAS”可证△ABF≌△DCE,可得∠ABF=∠DCE,可得结论;
(2)通过证明四边形FGMN是平行四边形,可得MG=NF;
(3)过点N作NH⊥MC于点H,由等腰三角形的性质可证∠BMG=∠MNH,可证∠GMN=90°,即可得四边形FGMN是矩形.
证明:(1)∵四边形ABCD是矩形
∴AB=CD,∠A=∠D=90°,且AF=DE
∴△ABF≌△DCE(SAS)
∴∠ABF=∠DCE,且∠ABC=∠DCB=90°
∴∠FBC=∠ECB
(2)∵FG=MN=CN
∴∠NMC=∠NCM
∴∠NMC=∠FBC
∴MN∥BF,且FG=MN
∴四边形FGMN是平行四边形
∴MG=NF
(3)四边形FGMN是矩形
理由如下:
如图,过点N作NH⊥MC于点H,
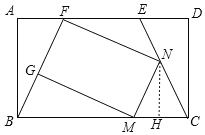
∵MN=NC,NH⊥MC
∴∠MNH=∠CNH=![]() ∠MNC,NH⊥MC
∠MNC,NH⊥MC
∴∠MNH+∠NMH=90°
∵∠MNC=2∠BMG,∠MNH=∠CNH=![]() ∠MNC
∠MNC
∴∠BMG=∠MNH,
∴∠BMG+∠NMH=90°
∴∠GMN=90°
∴四边形FGMN是矩形


科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
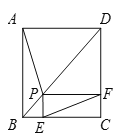
【题目】如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列三个结论:①AP=EF;②△APD一定是等腰三角形;③∠PFE=∠BAP.其中正确结论的序号是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
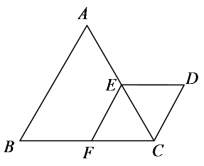
【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB.
(1)求证:四边形EFCD是菱形;
(2)设CD=2,求D、F两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末,历史老师为了了解所任教的甲、乙两班学生的历史基础知识背诵情况,从甲、乙两个班学生中分别随机抽取了20名学生来进行历史基础知识背诵检测,满分50分,得到学生的分数相关数据如下:
甲 | 32 | 35 | 46 | 23 | 41 | 49 | 37 | 41 | 36 | 41 |
37 | 44 | 39 | 46 | 46 | 41 | 50 | 43 | 44 | 49 |
乙 | 25 | 34 | 43 | 46 | 35 | 41 | 42 | 46 | 44 | 42 |
47 | 45 | 42 | 34 | 39 | 47 | 49 | 48 | 45 | 42 |
通过整理,分析数据:两组数据的平均数、中位数、众数如下表:
平均数(分) | 中位数(分) | 众数(分) | |
甲 | 41 | 41 |
|
乙 | 41.8 |
| 42 |
历史老师将乙班成绩按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示分数)绘制成扇形统计图,如图(不完整)
表示分数)绘制成扇形统计图,如图(不完整)
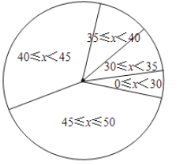
请回答下列问题:
(1)![]() _______分;
_______分;
(2)扇形统计图中,![]() 所对应的圆心角为________度;
所对应的圆心角为________度;
(3)请结合以上数据说明哪个班背诵情况更好(列举两条理由即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在△ABC 中,∠ABC 的平分线 BF 交 AC 于 F, 过点 F 作 DF∥BC, 求证:BD=DF.
(2)如图 2,在△ABC 中,∠ABC 的平分线 BF 与∠ACB 的平分线 CF 相交于 F,过点 F 作 DE∥BC,交直线 AB 于点 D,交直线 AC 于点 E.那么 BD,CE,DE 之间存在什么关系?并证明这种关系.
(3)如图 3,在△ABC 中,∠ABC 的平分线 BF 与∠ACB 的外角平分线 CF 相交于 F,过点 F 作 DE∥BC,交直线 AB 于点D,交直线 AC 于点 E.那么 BD,CE,DE 之间存在什么关系?请写出你的猜想.(不需证明)
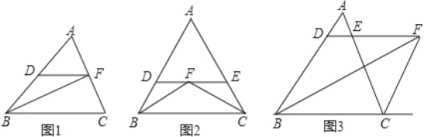
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com