
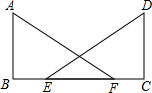
 已知:如图,∠B=∠C=90°,AF=DE,BE=CF.
已知:如图,∠B=∠C=90°,AF=DE,BE=CF. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
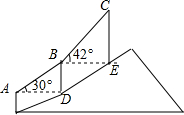 如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com