
如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数 (k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
解:(1)∵OA=OB=2,∴A(﹣2,0),B(0,2)。
将A与B的坐标代入y=k1x+b得: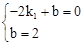 ,解得:
,解得: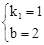 。
。
∴一次函数解析式为y=x+2。
(2)∵OD=2,∴D(2,0)。
∵点C在一次函数y=x+2上,且CD⊥x轴,
∴将x=2代入一次函数解析式得:y=2+2=4,即点C坐标为(2,4)。
∵点C在反比例图象上,∴将C(2,4)代入反比例解析式得:k2=8。
∴反比例解析式为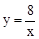 。
。
解析试题分析:(1)由OA与OB的长,确定出A与B的坐标,代入一次函数解析式中求出k1与b的值,即可确定出一次函数解析式。
(2)由OD的长,确定出D坐标,根据CD垂直于x轴,得到C与D横坐标相同,代入一次函数解析式求出C的纵坐标,确定出C坐标,将C坐标代入反比例解析式中求出k2的值,即可确定出反比例解析式。


科目:初中数学 来源: 题型:解答题
已知一次函数 的图象经过点
的图象经过点 ,且与函数
,且与函数 的图象相交于点
的图象相交于点 .
.
(1)求 的值;
的值;
(2)若函数 的图象与
的图象与 轴的交点是B,函数
轴的交点是B,函数 的图象与
的图象与 轴的交点是C,求四边形
轴的交点是C,求四边形 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
青海新闻网讯:西宁市为加大向国家环境保护模范城市大步迈进的步伐,积极推进城市绿地、主题公园、休闲场地建设.园林局利用甲种花卉和乙种花卉搭配成A、B两种园艺造型摆放在夏都大道两侧.搭配数量如下表所示:
| | 甲种花卉(盆) | 乙种花卉(盆) |
| A种园艺造型(个) |  盆 盆 |  盆 盆 |
| B种园艺造型(个) |  盆 盆 |  盆 盆 |
 元.若园林局搭配A种园艺造型
元.若园林局搭配A种园艺造型 个,B种园艺造型
个,B种园艺造型 个共投入
个共投入 元.则A、B两种园艺 造型的单价分别是多少元?
元.则A、B两种园艺 造型的单价分别是多少元? 个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过
个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过 盆,乙种花卉不超过
盆,乙种花卉不超过 盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
盆,问符合题意的搭配方案有几种?请你帮忙设计出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川南充8分)某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校为了实施“大课间”活动,计划购买篮球、排球共60个,跳绳120根.已知一个篮球70元,一个排球50元,一根跳绳10元.设购买篮球x个,购买篮球、排球和跳绳的总费用为y元.
(1)求y与x之间的函数关系式;
(2)若购买上述体育用品的总费用为4 700元,问篮球、排球各买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线AB分别与x轴,y轴相交于A,B两点,OA,OB的长分别是方程x2﹣14x+48=0的两根,且OA<OB.
(1)求点A,B的坐标.
(2)过点A作直线AC交y轴于点C,∠1是直线AC与x轴相交所成的锐角,sin∠1= ,点D在线段CA的延长线上,且AD=AB,若反比例函数
,点D在线段CA的延长线上,且AD=AB,若反比例函数 的图象经过点D,求k的值.
的图象经过点D,求k的值.
(3)在(2)的条件下,点M在射线AD上,平面内是否存在点N,使以A,B,M,N为顶点的四边形是邻边之比为1:2的矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线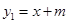 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,与双曲线
,与双曲线
 分别交于点
分别交于点 ,且
,且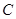 点的坐标为
点的坐标为 .
.
(1)分别求出直线 及双曲线的解析式;
及双曲线的解析式;
(2)求出点 的坐标;
的坐标;
(3)利用图象直接写出:当 在什么范围内取值时,
在什么范围内取值时,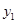 >
> .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com