
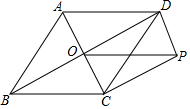
 如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.
如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.分析 (1)只要证明四边形OCPD是矩形,求出CD即可解决问题.
(2)四边形ABCD、四边形BOPC、四边形OCPD、四边形AOPD都是平行四边形.
解答 (1)解:∵DP∥AC,CP∥BD,
∴四边形OCPD是平行时四边形,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=OC=2,OB=OD=4,
∴∠COD=90°,
∴四边形OCPD是矩形,
∴CD=OP.
在Rt△COD中,易知CD=2$\sqrt{5}$,
∴OP=CD=2$\sqrt{5}$.
(2)四边形ABCD、四边形BOPC、四边形OCPD、四边形AOPD都是平行四边形.
点评 本题考查菱形的性质、平行四边形的判定和性质、矩形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}+3}{2}$ | C. | $\frac{\sqrt{3}+3}{4}$ | D. | $\frac{3\sqrt{3}+3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com