
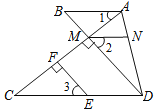
【题目】如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
【答案】证明见解析.
【解析】试题分析:因为EF⊥AC,DM⊥AC得到EF∥DM,根据平行线的性质得∠3=∠CDM,则∠2=∠CDM,根据平行线的判定得到MN∥CD,所以∠AMN=∠C,又∠1=∠C,于是∠1=∠AMN,然后根据平行线的判定得到AB∥MN.
试题解析:
∵EF⊥AC,DM⊥AC,
∴∠CFE=∠CMD=90°(垂直定义),
∴EF∥DM(同位角相等,两直线平行),
∴∠3=∠CDM(两直线平行,同位角相等)
∵∠3=∠2(已知)
∴∠2=∠CDM(等量代换)
∴MN∥CD(内错角相等,两直线平行)
∴∠AMN=∠C(两直线平行,同位角相等)
∵∠1=∠C(已知)
∴∠1=∠AMN(等量代换)
∴AB∥MN(内错角相等,两直线平行)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
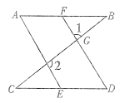
【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
A.![]()
B.![]()
C.π
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
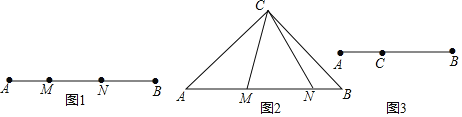
【题目】定义,如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N为线段AB的勾股分割点.
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=5,求BN的长
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,∠MCN=45°,求证:点M,N是线段AB的勾股分割点;阳阳在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把△CBN绕点C逆时针旋转90度试试,请根据陈老师的提示完成证明过程.
(3)如图3,C是线段AB上的一定点,请在BC上画一点D,使C、D是线段AB的勾股分割点
(要求:完成尺规作图,保留作图痕迹,并在右侧分步写出作图步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com