
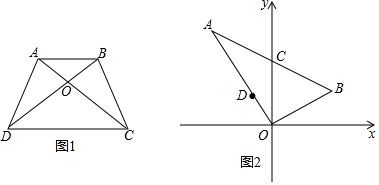
分析 (1)根据同底等高面积相等,即可解决问题;
(2)①求出直线AB的解析式可得点C坐标,即可解决问题;
②连接CD,过点O作OE∥CD交AB于点E,连接DE,则DE就是所作的线.
解答 解:(1)∵AB∥DC,
∴S△ABD=S△ABC,S△ADC=S△BDC,
∴S△AOD=S△BOC.
(2)∵点A(-2,3),B(2,1),
∴直线AB的解析式为y=-$\frac{1}{2}$x+2,
∴C(0,2)
∴S△AOC=$\frac{1}{2}$×2×2=2,S△BOC=$\frac{1}{2}$×2×2=2,
,
(3)连接CD,过点O作OE∥CD交AB于点E,连接DE,则DE就是所作的线.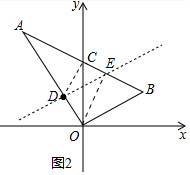
点评 本题考查梯形,坐标与图形的性质,一次函数的应用,等高模型等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{ax>1}\\{bx>1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{ax<2}\\{bx<2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{ax>3}\\{bx<3}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{ax<4}\\{bx>4}\end{array}}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
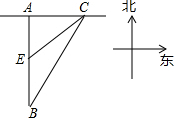
 “某市道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过60千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米C处,过了2秒后到达B处,测得小汽车与车速检测仪间距离为50米,请问这辆小汽车超速了吗?为什么?若超速,则超速了多少?
“某市道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过60千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米C处,过了2秒后到达B处,测得小汽车与车速检测仪间距离为50米,请问这辆小汽车超速了吗?为什么?若超速,则超速了多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15° | B. | 30° | C. | 30°或60° | D. | 30°或150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读材料,回答问题
阅读材料,回答问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com