
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
分析 (1)根据数轴a和b在数轴上的位置即可直接数出A和B之间的距离;
(2)根据d和a、b的大小即可直接得到三者之间的大小关系;
(3)到7和-7的距离之和为14的所有整数,就是7和-7之间的所有整数,然后求和;
(4)|x+1|+|x-2|表示数轴上的点到-1和到2的距离的和,据此即可确定;
(5)根据路程的和是15个单位长度,速度比是3:2,时间是3秒,即可求得二者的速度.
解答 解:(1)6,2,12;
(2)由(1)可得:d=|a-b|或d=b-a;
(3)所有满足条件的整数之和为:
-7+(-6)+(-5)+(-4)+(-3)+(-2)+(-1)+0+1+2+3+4+5+6+7=0;
(4)根据数轴的几何意义可得-1和2之间的任何一点均能使|x+1|+|x-2|取得的值最小.故可得:点C的范围在:-1≤x≤2时,能满足题意.
(5)设A的速度是3x个单位长度/秒,B的速度是2x个单位长度/秒.
根据题意得3(3x+2x)=15,
解得:x=1.
动点A运动的速度为3个单位长度/秒动点B运动的速度为2个单位长度/秒.
点评 本题考查了利用数轴表示有理数以及列方程解应用题,正确理解|x+1|+|x-2|表示数轴上的点到-1和到2的距离的和是关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
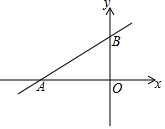 一次函数的图象与x轴、y轴分别交于点A(-4,0)和点B(0,3).
一次函数的图象与x轴、y轴分别交于点A(-4,0)和点B(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
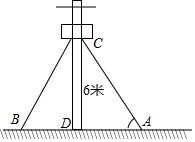 如图,在离地面6m的C处引拉线CB,CA固定电线杆,CA=CB,CD⊥AB于点D,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD.
如图,在离地面6m的C处引拉线CB,CA固定电线杆,CA=CB,CD⊥AB于点D,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com