
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
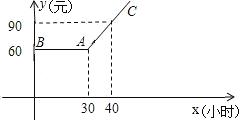
【答案】(1)y=3x﹣30;(2)4月份上网20小时,应付上网费60元;(3)5月份上网35个小时.
【解析】
(1)由图可知,当x≥30时,图象是一次函数图象,设函数关系式为y=kx+b,使用待定系数法求解即可;
(2)根据题意,从图象上看,30小时以内的上网费用都是60元;
(3)根据题意,因为60<75<90,当y=75时,代入(1)中的函数关系计算出x的值即可.
(1)当x≥30时,设函数关系式为y=kx+b,
则![]() ,
,
解得![]() ,
,
所以y=3x﹣30;
(2)若小李4月份上网20小时,由图象可知,他应付60元的上网费;
(3)把y=75代入,y=3x-30,解得x=35,
∴若小李5月份上网费用为75元,则他在该月份的上网时间是35小时.


科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图像交于点
的图像交于点![]() ,
,![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)结合函数图像,写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 的面积是
的面积是![]() 面积的3倍,请求出点
面积的3倍,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(3,0),B(0,3),过点B画y轴的垂线l,点C在线段AB上,连结OC并延长交直线l于点D,过点C画CE⊥OC交直线l于点E.
(1)求∠OBA的度数,并直接写出直线AB的解析式;
(2)若点C的横坐标为2,求BE的长;
(3)当BE=1时,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
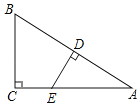
【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AB,AC于点D,E.
(1)求证:AE=2CE;
(2)当DE=1时,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
(1)若点P恰好在∠ABC的角平分线上,求出此时t的值;
(2)若点P使得PB+PC=AC时,求出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
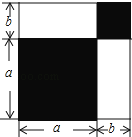
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com