
分析 根据题目中的例子解答前四问,第五问根据前面的规律去掉绝对值符号,然后再去掉括号解答即可.
解答 解:(1)根据题目中的信息,故答案为:|7-21|=21-7;
(2)根据题目中的信息,故答案为:|$-\frac{1}{2}+0.8$|=0.8-$\frac{1}{2}$;
(3)根据题目中的信息,故答案为:|$\frac{7}{17}-\frac{7}{18}$|=$\frac{7}{17}-\frac{7}{18}$;
(4)根据题目中的信息,故答案为:|$3.2-2.8-\frac{2}{3}$|=2.8+$\frac{2}{3}$-3.2;
(5)|$\frac{1}{5}-\frac{150}{557}$|+|$\frac{150}{557}-\frac{1}{2}$|-|$\frac{1}{5}$$-\frac{1}{2}$|
=$\frac{150}{557}$-$\frac{1}{5}$+$\frac{1}{2}$-$\frac{150}{557}$-($\frac{1}{2}$-$\frac{1}{5}$)
=$\frac{150}{557}$-$\frac{1}{5}$+$\frac{1}{2}$-$\frac{150}{557}$-$\frac{1}{2}$+$\frac{1}{5}$
=0.
点评 本题考查学生对绝对值的掌握和有理数的加减混合运算.


科目:初中数学 来源: 题型:解答题
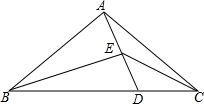 己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC.
己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com