
| 2 |
| 3 |
 60°-15°=45°.
60°-15°=45°.| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
30
| ||
| 60 |
| ||
| 2 |
| 60 |
| 72 |
| 5 |
| 6 |
| 5 |
| 6 |


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
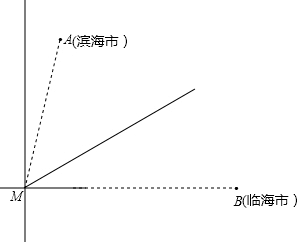
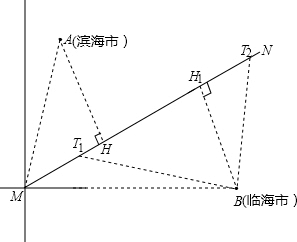
如图,在海面上生产了一股强台风,台风中心(记作点M)位于滨海市(记作点A)的南偏西15°,距离为![]() 千米,且位于临海市(记作点B)正西方向
千米,且位于临海市(记作点B)正西方向![]() 千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.
(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?
 |
查看答案和解析>>
科目:初中数学 来源:第21章《解直角三角形》中考题集(38):21.5 应用举例(解析版) 题型:解答题
 千米,且位于临海市(记作点B)正西方向
千米,且位于临海市(记作点B)正西方向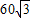 千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.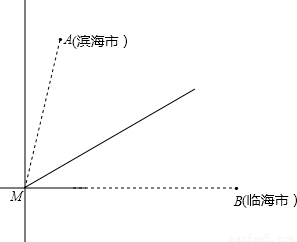
查看答案和解析>>
科目:初中数学 来源:第31章《锐角三角函数》中考题集(40):31.3 锐角三角函数的应用(解析版) 题型:解答题
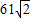 千米,且位于临海市(记作点B)正西方向
千米,且位于临海市(记作点B)正西方向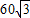 千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.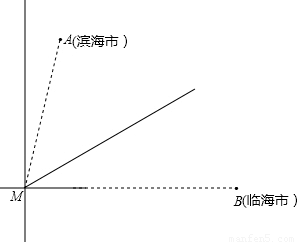
查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》中考题集(37):25.3 解直角三角形(解析版) 题型:解答题
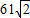 千米,且位于临海市(记作点B)正西方向
千米,且位于临海市(记作点B)正西方向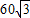 千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.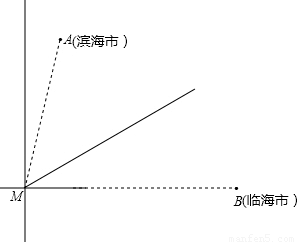
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com