
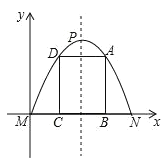
����Ŀ����ͼ����һ����Ƥ�����α�Ե��������״��MN=4�������߶��㴦����MN�ľ�����4��Ҫ����Ƥ�Ͻ���һ����ABCD��ʹ���ζ���B��C���ڱ�MN�ϣ�A��D�����������ϣ�
��1����ͼ�����ʵ�������ϵ���������߽���ʽ��
��2�������ABCD���ܳ�ΪL����C������Ϊ��m��0������L��m�Ĺ�ϵʽ����Ҫ��д�Ա���ȡֵ��Χ����
��3������������ȥ�ľ�����Ƥ���ܳ��ܷ����9.5����������9.5����˵�����ɣ�������9.5��������ֵ��

���𰸡���1��y=��x2+4x����2��L=��2m2+4m+8����3���ܵ���9.5����ʱm1=![]() ��m2=
��m2=![]() ��
��
���������������: ��1������MN=4�������߶��㵽MN�ľ�����4dm���õ�N��4��0����P��2��4����������ú����Ľ���ʽ��
��2����BC��DC��m��ʾ����������L=2��BC+DC�����ɣ�
��3����L=9.5����L=��2m2+4m+8���ⷽ�̼��ɣ�
�������:
�⣺��1����MN=4dm�������߶��㵽MN�ľ�����4dm��
��N��4��0��������P��2��4����
�������ߵĽ���ʽΪ��y=a��x��2��2+4��
��N��4��0������ã�0=a��4��2��2+4��
��ã�a=��1��
�������ߵĽ���ʽΪ��y=����x��2��2+4��
���������ߵĽ���ʽΪ��y=��x2+4x��
��2����C��������m��0����
��BC=4��2m��DC�T��m2+4m��
��L=2��BC+DC��=��2m2+4m+8��
��3���ܵ���9.5��
��L=��2m2+4m+8=9.5��
��2m2��4m+1.5=0��
��ã�m1=![]() ��m2=
��m2=![]() ��
��
�㾦: ������Ҫ�������ô���ϵ��������κ�������ʽ�����κ�����ʵ��Ӧ�ã����κ�����һԪ���η��̵Ĺ�ϵ������Ĺؼ��ǽ�ʵ������ת������ѧ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ��������ֻ���ϣ��������ڵ�A�����������ڵ�B����������ֻ����ͬʱ���������з���ֻ����ֱ��AB�������������������������ѡ���Ҽ��������е��ٶȱ������Ͽ죮(1)������ѡ�������������еĸ���Ϊ________��
(2)�����б�����״ͼ�ķ�������ֻ���Ͽ�ʼ���к�������������ĸ��ʣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲��������������½ϵ�ʱ����װ�к���ϵͳ�Ĵ�������һ������Ȼ�������¶�Ϊ18![]() ������������������Ʒ�֣���ͼ����ij�����ϵͳ�ӿ������رռ��رպ������¶�y(
������������������Ʒ�֣���ͼ����ij�����ϵͳ�ӿ������رռ��رպ������¶�y(![]() )��ʱ��x(Сʱ)�仯�ĺ���ͼ������BC����˫����
)��ʱ��x(Сʱ)�仯�ĺ���ͼ������BC����˫����![]() ��һ���֣������ͼ����Ϣ����������⣺
��һ���֣������ͼ����Ϣ����������⣺

(1)����ϵͳ���챣�ִ������¶�18![]() ��ʱ���ж���Сʱ��
��ʱ���ж���Сʱ��
(2)��kֵ��
(3)��x=15ʱ�������ڵ��¶�ԼΪ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
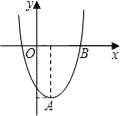
����Ŀ����ֱ������ƽ���ڣ����κ���ͼ��Ķ���ΪA��1����4�����ҹ���B��3��0����
��1����ö��κ����Ľ���ʽ��
��2�����ö��κ���ͼ������ƽ�Ƽ�����λ����ʹƽ�ƺ�����ͼ������ԭ�㣿��ֱ��д��ƽ�ƺ�����ͼ����x�����һ����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������ͼ���ݺ���ͼ��ش��������⣺
������ͼ���ݺ���ͼ��ش��������⣺
��1���б�����㡢����
x | |||||
|
��2��![]() ���������Ƕ��٣�
���������Ƕ��٣�
��3��xȡ��ֵʱ��y��0��
��4��xȡ��ֵʱ����������x���ϻ��·���
��5��������![]() ��ֱ��y=k��Ψһ�Ľ��㣬��k=�� ����
��ֱ��y=k��Ψһ�Ľ��㣬��k=�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��
��![]() ����ͼ�٣���֪������
����ͼ�٣���֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �����㣬��
�����㣬��![]() ������
������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ������
������![]() ��
��![]() ��λ�ù�ϵ����֤����Ľ��ۣ�
��λ�ù�ϵ����֤����Ľ��ۣ�
��![]() ����ͼ�ڣ���֪������
����ͼ�ڣ���֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ����������ͬ���ٶ���
ͬʱ����������ͬ���ٶ���![]() ��
��![]() �������յ�
�������յ�![]() ��
��![]() �˶�������
�˶�������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() �ܳ������ֵ��
�ܳ������ֵ��
������
��![]() ����ͼ����
����ͼ����![]() Ϊ�߳�Ϊ
Ϊ�߳�Ϊ![]() ������
������![]() �ĶԽ��ߣ�
�ĶԽ��ߣ� ![]() ����
����![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ����������ͬ���ٶ���
ͬʱ����������ͬ���ٶ���![]() ��
��![]() ���յ�
���յ�![]() ��
��![]() �˶�������
�˶�������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() �ܳ������ֵ��
�ܳ������ֵ��



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�˼������ͼ�� ![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϵ��������㣬��
�ϵ��������㣬��![]() ��
��![]() ��ֱ��
��ֱ��![]() ���˶�����
���˶�����![]() �ڵ�
�ڵ�![]() ����ࣩ��
����ࣩ��![]() ����֪
����֪![]() ��
�� ![]() ��
��![]() ��ľ���Ϊ
��ľ���Ϊ![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �۵���
�۵���![]() ��
��
��![]() ����
����![]() ��
��![]() �����غ�ʱ����
�����غ�ʱ����![]() __________
__________ ![]() ��
��
��![]() ����
����![]() ��
��![]() ���㲻�غ�ʱ��
���㲻�غ�ʱ��
������![]() ��̽��
��̽��![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
������![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��Σ�����ʾ��ͼ��ֱ��д��
Ϊ������ı����Ǿ��Σ�����ʾ��ͼ��ֱ��д��![]() �ij���
�ij���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ![]() ��һ����������ת����ת�̣����ֳ��������ȵ��������Σ��ֱ������
��һ����������ת����ת�̣����ֳ��������ȵ��������Σ��ֱ������![]() ��
�� ![]() ��
�� ![]() ����ת��һ��ת�̣�ת��ֹͣ��ָ��ָ��������ڵ�����Ϊ
����ת��һ��ת�̣�ת��ֹͣ��ָ��ָ��������ڵ�����Ϊ![]() �����ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ����ͼ
�����ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ����ͼ![]() �DZ�����ȫһ�����������ֱַ���
�DZ�����ȫһ�����������ֱַ���![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �������˿��ƣ��������˿��Ʊ��泯�ϣ�ϴ�Ⱥ���������ϣ���������һ���Ƶ��������ּ�Ϊ
�������˿��ƣ��������˿��Ʊ��泯�ϣ�ϴ�Ⱥ���������ϣ���������һ���Ƶ��������ּ�Ϊ![]() ������
������![]() ��ֵ��
��ֵ��


��![]() ������״ͼ���б�����
������״ͼ���б�����![]() �ĸ��ʣ�
�ĸ��ʣ�
��![]() ��������������Ϸ���涨����
��������������Ϸ���涨����![]() ������ʱ����ʤ��������ʤ������Ϊ�����Ϸ����Լ���˫����ƽ����˵�����ɣ�
������ʱ����ʤ��������ʤ������Ϊ�����Ϸ����Լ���˫����ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����MON=80�㣬OEƽ�֡�MON����A��B��C�ֱ�������OM��OE��ON�ϵĶ��㣨A��B��C�����O �غϣ�������AC������OE�ڵ�D�����OAC=x�㣮
��1����ͼ1����AB��ON���١�ABO�Ķ�������������������
����ͼ2������BAD=��ABDʱ������x��ֵ��Ҫ˵�����ɣ���
��2����ͼ3����AB��OM�����Ƿ����������X��ֵ��ʹ�á�ADB����������ȵĽǣ������ڣ�ֱ��д��x��ֵ���������ڣ�˵�����ɣ����Լ���ͼ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com