
| A. | a>b | B. | a=b | C. | a<b | D. | 无法确定 |
分析 先分母有理化得到a=$\frac{\sqrt{6}}{2}$+4<6,b=12$\sqrt{2}$+6$\sqrt{6}$>18,再根据实数大小比较的方法进行比较即可求解.
解答 解:∵a=$\frac{1}{{\sqrt{6}-2}}$=$\frac{\sqrt{6}+2}{(\sqrt{6}-2)(\sqrt{6}+2)}$=$\frac{\sqrt{6}}{2}$+4<6,
b=$\frac{12}{{\sqrt{8}-\sqrt{6}}}$=$\frac{12(\sqrt{8}+\sqrt{6})}{(\sqrt{8}-\sqrt{6})(\sqrt{8}+\sqrt{6})}$=6$\sqrt{8}$+6$\sqrt{6}$=12$\sqrt{2}$+6$\sqrt{6}$>18,
∴a<b.
故选:C.
点评 考查了分母有理化,关键是得到a=$\frac{\sqrt{6}}{2}$+4<6,b=12$\sqrt{2}$+6$\sqrt{6}$>18.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
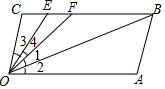 如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.
如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
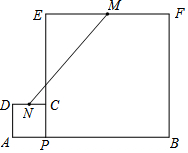 如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是5.
如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(m,2$\sqrt{2}$),B(3$\sqrt{2}$,0),C(n,-2$\sqrt{2}$),AC经过原点O,BH⊥AC于H,则AC•BH的值为24.
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(m,2$\sqrt{2}$),B(3$\sqrt{2}$,0),C(n,-2$\sqrt{2}$),AC经过原点O,BH⊥AC于H,则AC•BH的值为24.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM=2,CM=2+2$\sqrt{3}$.
在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM=2,CM=2+2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com