
 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分) (
(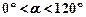 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△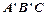 ,
, 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数;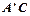 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交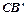 边于点E,联结BE.
边于点E,联结BE.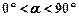 时,设
时,设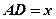 ,
,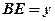 ,求
,求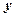 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域;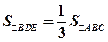 时,求
时,求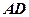 的长.
的长. 

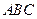 中,∵∠A=30°,
中,∵∠A=30°,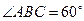 .………………………………………………………(1分)
.………………………………………………………(1分)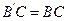 ,
,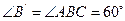 ,
,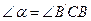
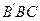 为等边三角形.……………(2分)
为等边三角形.……………(2分)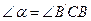 =
=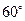 .……………(1分)
.……………(1分)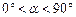 时,点D在AB边上(如图).
时,点D在AB边上(如图). 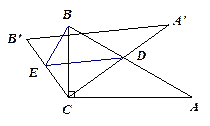
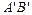 ,
,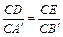 ..…………………………………………………(1分)
..…………………………………………………(1分)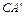 ,CB=
,CB=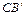 , ∠ACD=∠BCE.
, ∠ACD=∠BCE.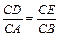 ,.…………………………………………………(1分)
,.…………………………………………………(1分)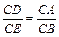 .
. E. .………………………………………(1分)
E. .………………………………………(1分)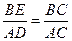 .
.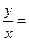
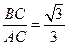 .……………………………………………(1分)
.……………………………………………(1分)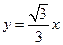 (0﹤
(0﹤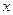 ﹤2)…………………………………………(2分)
﹤2)…………………………………………(2分)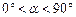 时,点D在AB边上
时,点D在AB边上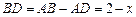 ,∠DBE=90°.
,∠DBE=90°.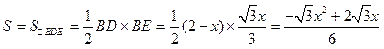 .
.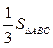 时,
时,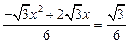 .
.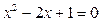 .
.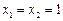 ,即AD="1." ……………………………
,即AD="1." …………………………… ……(2分)
……(2分)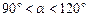 时,点D在AB的延长线上(如图)
时,点D在AB的延长线上(如图) .
.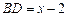 ,∠DBE=90°..
,∠DBE=90°..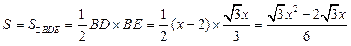 .
.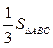 时,
时,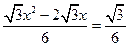 .
.
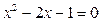 .
.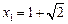 ,
,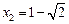 (负值,舍去).
(负值,舍去). 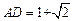 .…………………………………………………(2分)
.…………………………………………………(2分)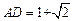 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
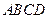 中,
中, ,
,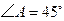 ,
,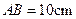 ,
, .等腰直角三角形
.等腰直角三角形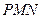 的斜边
的斜边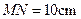 ,
,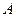 点与
点与 点重合,
点重合,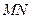 和
和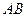 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形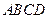 不动,等腰直角三角形
不动,等腰直角三角形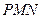 沿
沿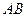 所在直线以
所在直线以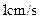 的速度向右移动,直到点
的速度向右移动,直到点 与点
与点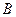 重合为止.
重合为止.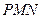 在整个移动过程中与等腰梯形
在整个移动过程中与等腰梯形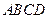 重叠部分的形状由 形
重叠部分的形状由 形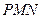 移动
移动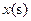 时,等腰直角三角形
时,等腰直角三角形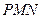 与等腰梯形
与等腰梯形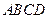 重
重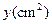 ,求
,求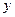 与
与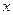 之间的函数关系式;
之间的函数关系式;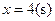 时,求等腰直角三角形
时,求等腰直角三角形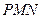 与等腰梯形
与等腰梯形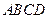 重叠部分的面积.
重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.矩形 | B.菱形 | C.正方形 | D.梯形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
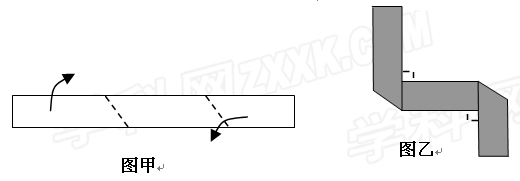
| A.60cm2 | B.58 cm2 | C.56 cm2 | D.54 cm2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

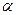 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).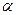 =30°时,求证:△AOE1为直角三角形.
=30°时,求证:△AOE1为直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com