
分析 用A、B、C、D、E、F、G分别表示“长跑”项目、“50米跑”项目、“一分钟跳绳”项目、“立定跳远”项目、“实心球”项目、“篮球”项目、“足球”项目,由于小亮、小明均选择“篮球”,所以两人四个测试项目可能为:ABDF、ABEF、ACDG、ACEF,用1、2、3、4分别表示四个测试项目,用画树状图展示所有16种等可能的结果,再找出小明与小刚选择同一种方案的结果数,然后利用概率公式求解即可.
解答 解:用A、B、C、D、E、F、G分别表示“长跑”项目、“50米跑”项目、“一分钟跳绳”项目、“立定跳远”项目、“实心球”项目、“篮球”项目、“足球”项目,
由于小亮、小明均选择“篮球”,两人四个测试项目可能为:ABDF、ABEF、ACDG、ACEF,用1、2、3、4分别表示四个测试项目,
画树状图为: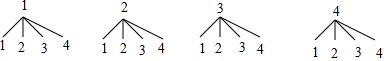
共有16种等可能的结果,小明与小刚选择同一种方案的有4种情况,
所以两人四个测试项目均相同的概率是$\frac{4}{16}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.


科目:初中数学 来源: 题型:解答题
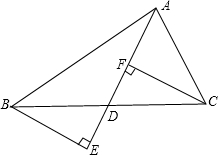 如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF⊥AD.
如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF⊥AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+1)2-5 | B. | y=2(x-1)2+1 | C. | y=2(x+1)2+1 | D. | y=2(x-1)2-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
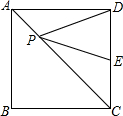 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )| A. | 3$\sqrt{10}$ | B. | 10$\sqrt{3}$ | C. | 9 | D. | 9$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com