练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．用配方法解方程x2-8x+15=0时，下列变形中，正确的是（　　）
    A．（x-4）2=31B．（x-4）2=1C．（x-8）2=1D．（x-8）2=31

    分析 先把15移到方程右边，再把方程两边加上16，然后把方程左边写成完全平方的形式即可．

    解答 解：x2-8x=-15，
    x2-8x+16=1，
    （x-4）2=1．
    故选B．

    点评 本题考查了解一元二次方程-配方法：将一元二次方程配成（x+m）2=n的形式，再利用直接开平方法求解，这种解一元二次方程的方法叫配方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．任意掷一枚质地均匀的骰子，掷出的点数是6的概率是$\frac{1}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

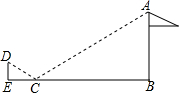    15．如图，为了测量旗杆AB的高度，小凡在距旗杆底部B点10.8米的C点处放置了一面镜子，当小凡行走到与BC位于同一直线的E点处时，恰好能从镜子中观察到旗杆顶部的A点．已知小凡眼睛所在的D点离地面的高度是1.6米，CE=2.7米，则旗杆AB的高度是（　　）
    A．6.4米B．7.2米C．8米D．9.6米

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若y=2$\sqrt{x-5}$+$\sqrt{5-x}$+2，则x-y=$\frac{1}{25}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，小亮在操场上玩，一段时间内沿M→A→B→M的路径匀速散步，能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

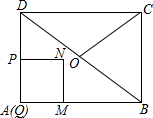    9．如图1，在矩形ABCD中，AB=4，BC=3，点O为对角线BD的中点，点P从点A出发，沿折线AD-DO以每秒1个单位长度的速度向终点O运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．
    （1）求点N落在BD上时t的值；
    （2）求出点O在正方形PQMN的任一边上时t的值；
    （3）当点P在折线AD-DO上运动时，求S与t之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．阅读下面的材料：
    在平面几何中，我们学过两条直线垂直的定义，下面就两个一次函数的图象所确定的两条直线，给出它们垂直的定义：设一次函数y=k1x+b1（k1≠0）的图象为直线l1，一次函数y=k2x+b2（k2≠0）的图象为直线l2，若k1•k2=-1，我们就称直线l1与直线l2互相垂直．
    解答下面的问题：
    （1）求过点P（4，1）且与已知直线y=-2x-1垂直的直线l的函数表达式，并画出直线l的图象；
    （2）设（1）中的直线l分别与y轴、x轴交于点A、B，如果直线m：y=kx+t（t＜0）与直线l垂直且交x轴于点C，求△ABC的面积S关于t的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

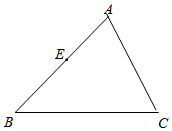    13．已知：如图，在△ABC中，过点A作AD⊥BC，垂足为D，E为AB上一点，过点E作EF⊥BC，垂足为F，过点D作DG∥AB交AC于点G．
    （1）依题意补全图形；
    （2）请你判断∠BEF与∠ADG的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

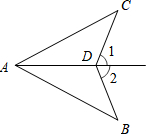    14．如图，∠1=∠2，那么添加一个条件后，仍无法判定△ABD≌△ACD的是（　　）
    A．AB=ACB．∠B=∠CC．ADAD平分∠CABD．CDCD=BD

    查看答案和解析>>

    同步练习册答案