练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．如图，小明想通过测量知道一建筑物AB的高度．他通过测量获得了以下的数据：站在点C处测得建筑物顶端A的仰角为48°，他的眼睛距离地面的高度CD=1.6m，C，B间的距离为12m．请你根据测量获得的数据，计算出建筑物AB的高度是多少？
    （参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11）

    分析 根据已知条件和正切值求出AE的长，再根据AB=AE+EB，即可得出答案．

    解答 解：作DE⊥AB于点E．
    ∵在直角△ABE中，∠ADE=48°，DE=BC=12（米），
    tan∠ADE=$\frac{AE}{DE}$，
    ∴AE=BE•tan∠ADE=12×1.11≈13.32米，
    ∴AB=AE+EB=14.92米．

    点评 本题考查仰角的定义，正切三角函数的定义，能借助仰角构造直角三角形并解直角三角形是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．计算$\sqrt{12}$+$\frac{6}{\sqrt{3}}$-$\root{3}{27}$的结果是4$\sqrt{3}$-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列计算正确的是（　　）
    A．$\sqrt{2}$+$\sqrt{2}$=2B．$\sqrt{3}$-$\sqrt{3}$=0C．$\sqrt{2}$×$\sqrt{2}$=4D．$\sqrt{（-3）^{2}}$=-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

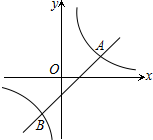    17．如图，已知A（4，2）、B（n，-4）是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点
    （1）求m的值和一次函数的解析式；
    （2）结合图象直接写出不等式$\frac{m}{x}$-kx-b＞0的解集；
    （3）若点M（t，y1）、N（1，y2）是反比例函数y=$\frac{m}{x}$上两点，且y1＜y2，请你借助图象，直接写出t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算
    （1）20160+$\sqrt{（-3）^{2}}$-（$\frac{1}{4}$）-1+3tan45°
    （2）解不等式组：$\left\{\begin{array}{l}{x-2＜2（x-1）}\\{\frac{x}{3}≤4-x}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

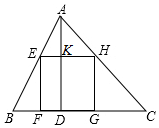    14．若正方形有两个相邻顶点在三角形的同一条边上，其余两个顶点分别在三角形的另两条边上，则正方形称为三角形该边上的内接正方形，△ABC中，设BC=a，AC=b，AB=c，各边上的高分别记为ha，hb，hc，各边上的内接正方形的边长分别记为xa，xb，xc
    （1）模拟探究：如图，正方形EFGH为△ABC的BC边上的内接正方形，求证：$\frac{1}{a}$+$\frac{1}{{h}_{a}}$=$\frac{1}{{x}_{a}}$；
    （2）特殊应用：若∠BAC=90°，xb=xc=2，求$\frac{1}{b}$+$\frac{1}{c}$的值；
    （3）拓展延伸：若△ABC为锐角三角形，b＜c，请判断xb与xc的大小，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．某公路的干线上有相距108公里的A、B两个车站，某日16点整，甲、乙两车分别从A、B两站同时出发，相向而行，已知甲车的速度为45公里/时，乙车的速度为36公里/时，则两车相遇的时间是（　　）
    A．16时20分B．17时20分C．17时40分D．16时40分

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如果4x-5y=0，且x≠0，那么$\frac{12x-5y}{12x+5y}$的值是$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

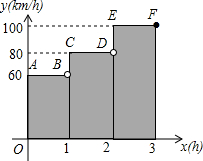    4．一辆汽车在某段路程中的行驶速度v（km/b）与时间t（h）的关系如图线段AB，CD，EF．
    （1）求图中阴影部分的面积．
    （2）说明所求阴影部分的面积的实际意义．
    （3）假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km，试求行驶这段路程时汽车里程表读数s（km）与时间t（h）的函数关系式．

    查看答案和解析>>

    同步练习册答案