
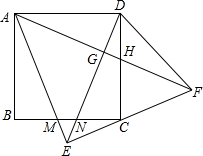
 如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 首先证明∠HCF=∠FHC=67.5°,由此可以判定③正确,②错误,再证明AC∥DF,推出S△DFA=S△FDC,由此判断⑤正确,根据ASA可以判断①正确,在△EAF中,由∠CAE=∠CAF,∠AEC=90°,作CK⊥AF于K,推出CE=CK<CF,由此判断④错误.
解答 解:如图,连接AC、以D为圆心DA为半径画圆.
∵四边形ABCD是正方形,
∴DA=DC=AB=BC,∠ADC=∠B=∠DCB=90°,∠ACD=∠DAC=45°
∵△DEF是由△DEA翻折得到,
∴DA=DF=DC,EA=EF,∠AED=∠DEF,
∴∠AFC=$\frac{1}{2}$∠ADC=45°
∴∠EFA=∠EAF=45°,
∴∠AEF=90°,
∴∠DEF=∠DEA=45°,
∵EA=ED=EF,
∴∠DAE=∠ADE=∠EDF=∠EFD=67.5°,
∴∠DAF=∠DFA=22.5°,
∴∠ADF=180°-∠DAF-∠DFA=135°,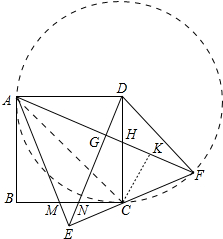
∴∠CDF=∠ADF-∠ADC=45°,
∴∠DCF=180°-∠CDF-∠DFC=67.5°,
∵∠CHF=∠CDF+∠DFA=67.5°,
∴∠HCF=∠FHC,
∴△CFH是等腰三角形,故③正确.②错误,
∵∠ACD=∠CDF,
∴AC∥DF,
∴S△DFA=S△FDC,
∴S△ADH=S△CHF,故⑤正确,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠BAM=∠CDN,
在△ABM和△DCN中,
$\left\{\begin{array}{l}{∠BAM=∠CDN}\\{AB=DC}\\{∠B=∠DCN}\end{array}\right.$,
∴△ABM≌△DCN,故①正确,
在△EAF中,∵∠CAE=∠CAF,∠AEC=90°,作CK⊥AF于K,
∴CE=CK<CF,
∴CE≠CF故④错误.
∴①③⑤正确,
选B.
点评 本题考查四边形综合题、圆的有关性质、全等三角形的判定和性质、平行线的性质等知识,解题的关键是添加辅助线,构造圆利用圆的有关性质解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
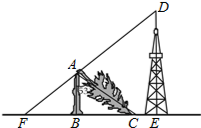 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
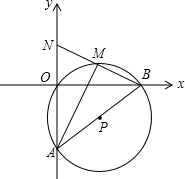 如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
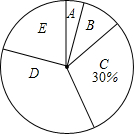 某学校为了解学生进行体育锻炼的情况,对某班学生每天的体育锻炼时间进行了统计,并绘制了以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
某学校为了解学生进行体育锻炼的情况,对某班学生每天的体育锻炼时间进行了统计,并绘制了以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:| 分组 | 锻炼时间(分钟) | 频数 |
| A | 20≤x<30 | 2 |
| B | 30≤x<40 | 5 |
| C | 40≤x<50 | 15 |
| D | 50≤x<60 | m |
| E | 60≤x<70 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com