
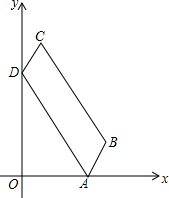
 如图,在?ABCD中,∠BAD=60°,点A在x轴的正半轴上,点D在y轴的正半轴上,tan∠OAD=$\sqrt{3}$,AD和DC的长分别是方程x2-8x+12=0的两个根(AD>DC).
如图,在?ABCD中,∠BAD=60°,点A在x轴的正半轴上,点D在y轴的正半轴上,tan∠OAD=$\sqrt{3}$,AD和DC的长分别是方程x2-8x+12=0的两个根(AD>DC).分析 (1)求出已知方程的解确定出AD与DC的长,在直角三角形AOD中,利用锐角三角函数定义求出∠OAD的度数,进而得到∠ADO的度数,利用30度所对的直角边等于斜边的一半求出OA的长,确定出A的坐标即可;
(2)过C作CE⊥y轴,过B作BF⊥x轴,分别在直角三角形CDE与直角三角形ABF中,利用30度所对的直角边等于斜边的一半求出CE与AF的长,利用勾股定理求出DE与BF的长,由OD+DE求出OE的长,由OA+AF求出OF的长,确定出B与C坐标,设直线BC解析式为y=kx+b,把B与C坐标代入求出k与b的值,即可确定出直线BC解析式;
(3)在坐标平面内存在一点N,使O,A,M,N为顶点的四边形是菱形,理由为:如图所示,分三种情况,四边形OAMN为菱形;四边形OAM′N′为菱形;四边形OAM′N″为菱形,利用菱形的性质及等边三角形的性质确定出满足题意N的坐标即可.
解答  解:(1)∵AD和DC的长分别是方程x2-8x+12=0的两个根(AD>DC),
解:(1)∵AD和DC的长分别是方程x2-8x+12=0的两个根(AD>DC),
∴AD=6,DC=2,
在Rt△AOD中,tan∠OAD=$\sqrt{3}$,
∴∠OAD=60°,
∴∠ADO=30°,
∴OA=$\frac{1}{2}$AD=3,
则A(3,0);
(2)过C作CE⊥y轴,过B作BF⊥x轴,
∵∠DAB=60,∠ADC=120°,
∴∠EDC=∠ABF=30°,
在Rt△DCE和Rt△ABF中,CD=AB=2,
∴CE=AF=1,
根据勾股定理得:DE=BF=$\sqrt{3}$,
∴OE=OD+DE=3$\sqrt{3}$+$\sqrt{3}$=4$\sqrt{3}$,即C(1,4$\sqrt{3}$),
OF=OA+AF=3+1=4,即B(4,$\sqrt{3}$),
设直线BC解析式为y=kx+b,
把B与C坐标代入得:$\left\{\begin{array}{l}{4k+b=\sqrt{3}}\\{k+b=4\sqrt{3}}\end{array}\right.$,
解得:k=-$\sqrt{3}$,b=5$\sqrt{3}$,
则直线BC解析式为y=-$\sqrt{3}$x+5$\sqrt{3}$;
(3)在坐标平面内存在一点N,使O,A,M,N为顶点的四边形是菱形,如图所示,
分三种情况考虑:
(i)四边形OAMN为菱形,可得ON=OA=AM=MN=3,
∵ON=OA=3,∠OAN=60°,
∴△OAN为等边三角形,
∴此时N($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$);
(ii)四边形OAM′N′为菱形,可得M′N′=AN′=OA=OM′=3,此时N′($\frac{9}{2}$,-$\frac{3\sqrt{3}}{2}$);
(iii)四边形OAM′N″为菱形,可得M′N″=AM′=OA=ON″=3,此时N″(-$\frac{3}{2}$,-$\frac{3\sqrt{3}}{2}$),
综上,N的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$)或($\frac{9}{2}$,-$\frac{3\sqrt{3}}{2}$)或(-$\frac{3}{2}$,-$\frac{3\sqrt{3}}{2}$).
点评 此题属于一次函数综合题,涉及的知识有:一元二次方程的解法,坐标与图形性质,待定系数法确定一次函数解析式,含30度直角三角形的性质,菱形的性质,以及等边三角形的性质,熟练掌握待定系数法是解本题第二问的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
 如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速前行,到达位于灯塔B的北偏东15°方向上的C处.
如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速前行,到达位于灯塔B的北偏东15°方向上的C处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 贷款日期 | 月利率% | 还款日期 | 贷款金额(万元) | 还款金额(万元) |
| 4月1日 | 1.5 | 12月1日 | ||
| 6月1日 | 1 | 12月1日 | ||
| 合计 | 300 | 330 |
| A(元) | B(元) | |
| 单件成本 | 3000 | 2000 |
| 单件出厂价 | 6500 | 6000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com