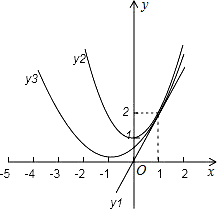
已知一次函数y1=2x和二次函数y2=x2+1.
(1)求证:函数y1、y2的图象都经过同一个定点;
(2)求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1≤y2总成立;
(3)是否存在抛物线y3=ax2+bx+c,其图象经过点(-5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1≤y3≤y2总成立?若存在,求出y3的解析式;若不存在,说明理由.
解:(1)令y
1=y
2,
得:2x=x
2+1,
整理得:x
2-2x+1=0
∵△=b
2-4ac=(-2)
2-4=0
∴直线y
1=2x与抛物线y
2=x
2+1只有一个交点,
即:函数y
1、y
2的图象都经过同一个定点;
(2)在实数范围内,对于x的同一个值y
2=x
2+1=(x-1)
2+2x,y
1=2x,
∵(x-1)
2≥0,
∴y
1≤y
2;
(3)由y
1=2x,y
2=x
2+1得:
y
2-y
1=x
2+1-2x=(x-1)
2即当x=1时,有y
1=y
2=2.
所以(1,2)点为y
1和y
2的交点.
因为要满足y
1≤y
3≤y
2恒成立,所以y
3图象必过(1,2)点.
又因为y
3-y
1=ax
2+bx+c-2x恒大于等于0,即ax
2+(b-2)x+c恒大于等于0,所以二次函数ax
2+(b-2)x+c必定开口向上,
即有a>0且(b-2)
2-4ac≤0,
同样有y
2-y
3=(1-a)x
2-bx+(1-c)恒大于0,
有 1-a>0 且 b
2-4(1-a)(1-c)≤0,
又因为函数过(-5,2)和(1,2)两点,所以有
25a-5b+c=2 ①
a+b+c=2 ②
①-②得 b=4a,
将b=4a代入②得:c=2-5a,
代入(b-2)
2-4ac≤0得,
(4a-2)
2-4a(2-5a)=16a
2-16a+4-8a+20a
2=36×a
2-24a+4=4(3a-1)
2≤0
等式成立时 a=

,
将b=4a,c=2-5a 代入b
2-4(1-a)(1-c)≤0,
(4a)
2-4(1-a)(1-(2-5a))=36×a
2-24a+4=4(3a-1)
2≤0
满足条件a=

所以y
3的解析式为y
3=

(x
2+4a+1)=

x2+

x+

.
分析:(1)令y
1=y
2,得到2x=x
2+1,得到其根的判别式等于0即可说明两图象只有一个交点,即经过同一个定点.
(2)把y
2化成完全平方的形式与y
1进行比较即可得出结论;
(3)由图可知,在实数范围内,对于x的同一个值,三个函数所对应的函数值y
1≤y
3≤y
2均成立,利用c=2-5a,代入(b-2)
2-4ac≤0得出a的值,于是可推理出抛物线的解析式.
点评:此题主要考查了二次函数与一元二次方程的关系、根的判别式、完全平方公式、非负数的性质以及用待定系数法确定函数解析式的方法,难度较大.


 ,
,
 (x2+4a+1)=
(x2+4a+1)= x2+
x2+ x+
x+ .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案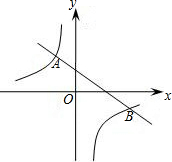 2,4)、(4,-2).
2,4)、(4,-2). (2012•德阳)已知一次函数y1=x+m的图象与反比例函数y2=
(2012•德阳)已知一次函数y1=x+m的图象与反比例函数y2= 已知一次函数y1=ax+b的图象与反比例函数y2=
已知一次函数y1=ax+b的图象与反比例函数y2= 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )