
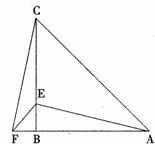
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证: Rt△AB E≌Rt△CBF;
E≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.
科目:初中数学 来源: 题型:
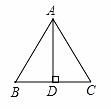
如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
|
| A. | AB=AC | B. | ∠BAC=90° | C. | BD=AC | D. | ∠B=45° |
查看答案和解析>>
科目:初中数学 来源: 题型:
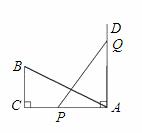
如图,Rt△ABC中,∠C=90°,AC=8,BC=4,PQ=AB,点P与点Q分别在AC和AC的垂线AD上移动,则当AP=_______时,△ABC≌△APQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
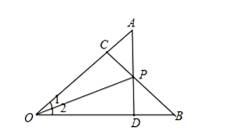
如图,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是( )
|
| A. | ∠1=∠2 | B. | ∠1>∠2 | C. | ∠1<∠2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
有一些整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如:22,131,1991,123321,…,像这样的 数,我们叫它“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”,办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文
数,我们叫它“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”,办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文 数,比如:
数,比如:
①132+231=363
②7299+9927=17226,17226+62271=79497,成功了!
(1)你能用上述方法,将下列各数“变”成回文数吗?
①237  ②362
②362
(2)请写出一个四位数,并用上述方法将它变成回文数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com