
【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④
【答案】C
【解析】解:①∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为x=﹣ ![]() =1,
=1,
∴b=﹣2a>0,①错误;
②∵b=﹣2a,a<0,
∴2a﹣b=2a﹣(﹣2a)=4a<0,②错误;
③根据函数图象可知:当x=1时,y>0,
∴a+b+c>0,③正确;
④根据函数图象可知:当x=﹣1时,y<0,
∴a﹣b+c<0,④正确;
⑤根据函数图象可知:当x>1时,y随x的增大而减小,⑤正确.
综上可知:正确的结论有③④⑤.
故选C.
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac
其中正确的结论的有( )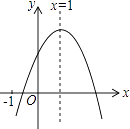
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
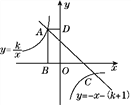
【题目】如图,长方形ABOD的顶点A是函数y=-x-(k+1)的图象与函数y=![]() 在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
(1)求两函数的表达式;
(2)求两函数图象的交点A,C的坐标;
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校、文具店、书店依次坐落在一条南北走向的大街上,学校在文具店的南边20 m处,书店在文具店的北边100 m处,张明同学从文具店出发,向北走了50 m,接着又向北走了-70 m,此时张明的位置在( )
A. 文具店 B. 学校 C. 书店 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
①四边形ABCD是菱形;
②四边形ABCD是中心对称图形;
③四边形ABCD是轴对称图形;
④AC=BD.
其中正确的是(写上正确的序号).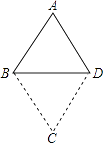
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条不完整的数轴上从左到右有A、B、C三个点,其中AB=3,BC=4,设点A、B、C所对应的数的和是p.
(1)若以B为原点,写出点A、C所对应的数,并计算p的值;若以C为原点,p的值为 .
(2)若原点O在图中数轴主点A的左侧,且BO=22,求p的值;
(3)若原点O在图中数轴上点B的右侧,且CO=a(a>0),求p的值(用含a的代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点H,G,连接DH,BG.
(1)求证:△AEH≌△CFG;
(2)连接BE,若BE=DE,则四边形BGDH是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内的一点,且PA=5,PB=4,PC=3,将△APB绕点B逆时针旋转,得到△CQB.求: 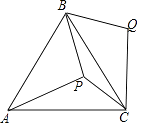
(1)点P与点Q之间的距离;
(2)求∠BPC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com