
 如图,在四边形EBCF中,点A为EF的中点,AB=AC,∠BAC=90°,BE=4$\sqrt{2}$,CF=5$\sqrt{2}$,EF=6,求△ABE的面积.
如图,在四边形EBCF中,点A为EF的中点,AB=AC,∠BAC=90°,BE=4$\sqrt{2}$,CF=5$\sqrt{2}$,EF=6,求△ABE的面积. 分析 首先根据题意寻找可以证明△AEB≌△CFA的条件,再利用全等三角形的性质可以得到AE=CF,BE=AF,再用勾股定理
解答 解:如图,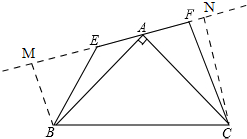
过点B作BM⊥EF,过点C作CN⊥EF,
∴∠AMB=∠CNA=90°.
∴∠MAB+∠MBA=90°.
又∵∠BAC=90°,
∴∠MAB+∠CAN=90°.
∴∠MBA=∠CAN.
在△AMB和△CNA中$\left\{\begin{array}{l}{∠AMB=∠CNA}\\{∠MBA=CAN}\\{AB=AB}\end{array}\right.$
∴△AMB≌△CNA,
∴AM=CN,BM=AN,
∵BE=4$\sqrt{2}$,CF=5$\sqrt{2}$,
∴MN=AN+AM=BM+CN,
∵点A为EF的中点,
∴AE=AF=$\frac{1}{2}$EF=3,
∴CN=AM=ME+3
FN=AN-AF=AN-3=BM-3
在Rt△BME中,BM2+ME2=BE2,
BM2+ME2=32①,
在Rt△CFN中,CN2+FN2=CF2
(ME+3)2+(BM-3)2=50②,
由①②得,ME=BM=4,
∴△ABE的面积=$\frac{1}{2}$×AE×BM=$\frac{1}{2}$×3×4=6.
点评 此题面积与等积变换,主要考查了三角形全等的判定及性质,解决问题的关键是证明△AEB≌△CFA.


科目:初中数学 来源: 题型:填空题
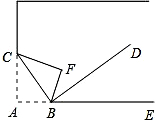 小东将书折过来,该角顶点A落在F处,BC为折痕,如图所示,若DB平分∠FBE,∠DBE比∠CBA大30°,设∠CBA和∠DBE分别为x°、y°,那么可求出这两个角的度数的方程组是$\left\{\begin{array}{l}{2x+2y=180}\\{y-x=30}\end{array}\right.$.
小东将书折过来,该角顶点A落在F处,BC为折痕,如图所示,若DB平分∠FBE,∠DBE比∠CBA大30°,设∠CBA和∠DBE分别为x°、y°,那么可求出这两个角的度数的方程组是$\left\{\begin{array}{l}{2x+2y=180}\\{y-x=30}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
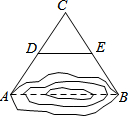 如图,A,B两点位于一个池塘的两端,冬冬想用绳子测量A,B两点间的距离,但绳子不够长,一位同学帮他想了一个办法:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测得DE的长为15m,则A,B两点间的距离为( )
如图,A,B两点位于一个池塘的两端,冬冬想用绳子测量A,B两点间的距离,但绳子不够长,一位同学帮他想了一个办法:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测得DE的长为15m,则A,B两点间的距离为( )| A. | 7.5m | B. | 15m | C. | 22.5m | D. | 30m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明在楼高AB=15米的楼顶A处测得一电视塔底部C的俯角为31°,测得塔高D的仰角为52°,求楼顶A对塔顶D的距离(结果保留整数)(参考数据:sin31°=0.52,cos 31°=0.86,tan 31°=0.80,sin52°=0.79,cos 52°═0.62,tan52°=1.28)
小明在楼高AB=15米的楼顶A处测得一电视塔底部C的俯角为31°,测得塔高D的仰角为52°,求楼顶A对塔顶D的距离(结果保留整数)(参考数据:sin31°=0.52,cos 31°=0.86,tan 31°=0.80,sin52°=0.79,cos 52°═0.62,tan52°=1.28)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0既不是正数,也不是负数 | B. | 当a>1时,则a的倒数大于0且小于1 | ||
| C. | a与-a互为相反数 | D. | |a|表示正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m,若灯泡距离地面2m,则地面上阴影部分的面积为1.44πm2.
如图所示,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m,若灯泡距离地面2m,则地面上阴影部分的面积为1.44πm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于F.
如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 知者加速:
知者加速:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com