练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知a2﹣b2＝6，a+b＝2，则a﹣b的值为（　　）

    A. 1B. 2C. 3D. 4

    【答案】C

    【解析】

    根据整式的混合运算，即可解答

    ∵a2﹣b2＝（a+b）（a﹣b）＝6，a+b＝2，∴a﹣b＝3，故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

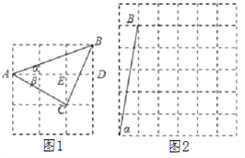
    【题目】(1)如图1，如果ɑ，β都为锐角，且tanɑ=，tanβ=，则ɑ+β=___________；

    (2)如果ɑ，β都为锐角，当tanɑ=5，tanβ=时，在图2的正方形网格中，利用已作出的锐角ɑ，画出∠MON，使得∠MON=ɑ-β.此时ɑ-β=__________度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有如图所示的甲、乙、丙长方形卡片若干张，用它们可以拼一些新的长方形．求长为（a+2b），宽为（2a+b）的长方形面积；若要拼这样一个长方形，则需要甲、乙、丙长方形卡片分别多少张？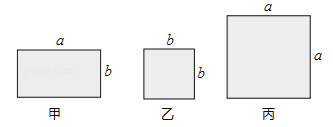

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若m=2100 ， n=375 ， 则m，n的大小关系为（ ）
    A.m＞n
    B.m＜n
    C.m=n
    D.无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

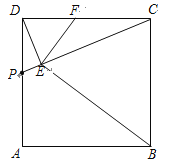
    【题目】如图，正方形ABCD中，点P是AD上的一动点（与点D、点A不重合），DE⊥CP，垂足为E，EF⊥BE与DC交于点F．

    （1）求证：△DEF∽△CEB；

    （2）当点P运动到DA的中点时，求证：点F为DC的中点.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据已知求值．
    （1）已知3×9m×27m=316 ， 求m的值．
    （2）已知am=2，an=5，求a2m﹣3n的值．
    （3）已知2x+5y﹣3=0，求4x32y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若点A（m﹣3，m+2）在y轴上，则点A到原点的距离为个单位长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下列材料，然后解答问题：
    材料1　从3张不同的卡片中选取2张排成一列，有6种不同的排法，抽象成数学问题就是从3个不同元素中选取2个元素的排列，排列数记为A32＝3×2＝6.
    一般地，从n个不同元素中选取m个元素的排列数记作Anm ，
    Anm＝n(n－1)(n－2)…(n－m＋1)(m≤n)．
    例：从5个不同元素中选3个元素排成一列的排列数为：A53＝5×4×3＝60.
    材料2　从3张不同的卡片中选取2张，有3种不同的选法，抽象成数学问题就是从3个元素中选取2个元素的组合，组合数记为C32＝＝3.
    一般地，从n个不同元素中选取m个元素的组合数记作Cnm ，
    Cnm＝ (m≤n)．
    例：从6个不同元素中选3个元素的组合数为：
    C63＝＝20.
    问：(1)从7个人中选取4人排成一排，有多少种不同的排法？
    (2)从某个学习小组8人中选取3人参加活动，有多少种不同的选法？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解
    材料一：一组对边平行，另一组对边不平行的四边形叫梯形，其中平行的两边叫梯形的底边，不平行的两边叫梯形的腰，连接梯形两腰中点的线段叫梯形的中位线．梯形的中位线具有以下性质：
    梯形的中位线平行于两底，并且等于两底和的一半．
    如图（1）：在梯形ABCD中：AD∥BC
    ∵E、F是AB、CD的中点
    ∴EF∥AD∥BC
    EF=（AD+BC）
    材料二：经过三角形一边的中点与另一边平行的直线必平分第三边
    如图（2）：在△ABC中：
    ∵E是AB的中点，EF∥BC
    ∴F是AC的中点
    如图（3）在梯形ABCD中，AD∥BC，AC⊥BD于O，E、F分别为AB、CD的中点，∠DBC=30°

    请你运用所学知识，结合上述材料，解答下列问题．
    （1）求证：EF=AC；
    （2）若OD=，OC=5，求MN的长．

    查看答案和解析>>

    同步练习册答案