
分析 根据反比例函数图象上点的坐标特征得到x1=$\frac{a}{{y}_{1}}$,x2=$\frac{a}{{y}_{2}}$,则$\frac{a}{{y}_{2}}$-$\frac{a}{{y}_{1}}$=8,而$\frac{1}{{y}_{2}}$-$\frac{1}{{y}_{1}}$>2,所以0<a<4,再把a-b=2代入a2-ab-c2+2c=0得到2a-c2+2c=0,则a=$\frac{{c}^{2}-2c}{2}$,所以0<$\frac{c(c-2)}{2}$<4,然后利用c的取值范围确定满足条件的整数.
解答 解:∵点P(x1,y1),Q(x2,y2)在反比例函数y=$\frac{a}{x}$(a≠0)图象上,
∴y1=$\frac{a}{{x}_{1}}$,y2=$\frac{a}{{x}_{2}}$,
∴x1=$\frac{a}{{y}_{1}}$,x2=$\frac{a}{{y}_{2}}$,
∵x2-x1=8,
∴$\frac{a}{{y}_{2}}$-$\frac{a}{{y}_{1}}$=8,
而$\frac{1}{{y}_{2}}$-$\frac{1}{{y}_{1}}$>2,
∴$\frac{8}{a}$>2,
∴0<a<4,
∵a-b=2,a2-ab-c2+2c=0,
∴2a-c2+2c=0,则a=$\frac{{c}^{2}-2c}{2}$,
∴0<$\frac{c(c-2)}{2}$<4,即0<c(c-2)<8,
当c<0时,c=-1;
当c>2时,c=3,
∴整数c的值的值为-1或3,
故答案为:-1或3.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.解决本题的关键是代数式的变形能力和解不等式组.


科目:初中数学 来源: 题型:解答题
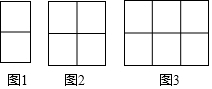
| 图形编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 图形中棋子的枚数 | 6 | 9 | 12 | 15 | 18 | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
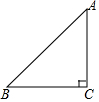 如图,△ABC是等腰直角三角形,∠C=90°.
如图,△ABC是等腰直角三角形,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
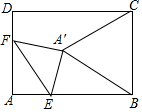 如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2$\sqrt{3}$,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为4或4$\sqrt{3}$.
如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2$\sqrt{3}$,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为4或4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com