
【题目】按要求解下列各题:
(1)先化简,再求值:5(a2b + 2ab2)- 2(3a2b + 4ab2-1),其中|a-2|+(b+ 3)2= 0:
(2)解方程:![]() =1-
=1-![]() .
.
【答案】(1)-a2b+2ab2+2;50;(2)![]() .
.
【解析】
(1)先根据去括号法则和合并同类项法则将整式化简,然后根据非负性求出a和b,代入求值即可;
(2)去分母、去括号、移项、合并同类项、系数化1即可.
解:(1)5(a2b + 2ab2)- 2(3a2b + 4ab2-1)
=5a2b+10ab2 - 6a2b -8ab2+2
= -a2b+2ab2+2
∵|a-2|+(b+ 3)2= 0,|a-2|≥0,(b+ 3)2≥0
∴a=2,b=-3
将a=2,b=-3代入,得
原式=-22×(-3)+2 ×2×(-3)2+2
=12+36+2
=50
(2)![]() =1-
=1-![]()
去分母,得![]()
去括号,得![]()
移项,得![]()
合并同类项,得![]()
系数化1,得![]()


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连接BD,过点E作EH⊥BD,垂足为H,连接EF,交BD于点G,交BC于点M,连接CF. 给出下列结论:①△CDE∽△CBF;②∠DBC=∠EFC;③ ![]() ;④GH的值为定值
;④GH的值为定值![]() ;上述结论中正确的个数为( )
;上述结论中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以正方形![]() 的顶点
的顶点![]() 为坐标原点,直线
为坐标原点,直线![]() 为
为![]() 轴建立直角坐标系,对角线
轴建立直角坐标系,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 上一点,点
上一点,点![]() 坐标为
坐标为![]() ,则点
,则点![]() 绕点
绕点![]() 顺时针旋转90°得到的对应点
顺时针旋转90°得到的对应点![]() 的坐标是( )
的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三边长分别为
三边长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点
,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点![]() (
(![]() 各个顶点都在网格的格点上).如图1所示,这样借用网格(不需
各个顶点都在网格的格点上).如图1所示,这样借用网格(不需![]() 的高)就能算出三角形的面积,这种方法叫构造法.
的高)就能算出三角形的面积,这种方法叫构造法.
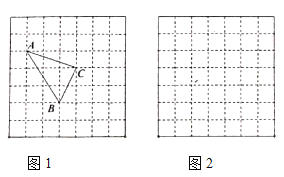
(1)![]() 的面积为___________________.
的面积为___________________.
(2)若![]() 的三边长分别为
的三边长分别为![]() 、
、![]() 、
、![]() ,请在图2的网格中画出
,请在图2的网格中画出![]() ,使得
,使得![]() 的三个顶点都在格点上,求此三角形的面积.
的三个顶点都在格点上,求此三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在直线1上,AB = 20cm,∠BAC= 120°.

(1)点P从A出发,沿射线AB以每秒2cm的速度向右运动,同时点Q从B出发,沿射线BA以每秒lcm的速度向左运动,求点P出发多少秒时与点Q重合?
(2)在(1)的条件下,求点P出发多少秒时与点Q相距5cm?
(3)点M为射线AC上一点,AM = 4cm,现将射线AC绕点A以每秒30°的速度顺时针旋转一周后停止,同时点N从点B出发沿直线AB向左运动,在这一运动过程中,是否存在某一时刻,使得点N为BM的中点?若存在,求出点N运动的速度:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )

A.5B.6C.4D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com