
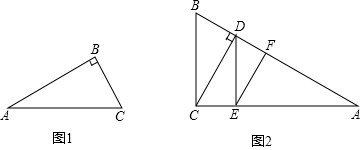
分析 (1)根据三角形的内角和得到∠B=60°,根据直角三角形的性质即可得到结论;
(2)根据平行线的性质得到∠AED=90°,∠AFE=∠ADC=90°,根据直角三角形的性质得到DF=12DE,AF=32DE,然后根据勾股定理即可得到结论.
解答 解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠BCD=30°,
∴BC=2BD=4,
∴AB=2BC=8cm;
故答案为:8;
(2)∵DE∥BC,
∴∠AED=90°,
∵AD=2DE,
∵EF∥CD,
∴∠AFE=∠ADC=90°,
∴∠DEF=30°,
∴DF=$\frac{1}{2}$DE,
∴AF=$\frac{3}{2}$DE,
∵AF比DF多2cm,
∴DE=2cm,
∴AD=4cm,
∵AB=2BC,BC2=AB•BD,
∴($\frac{1}{2}$AB)2=AB•(AB-4),
∴AB=$\frac{16}{3}$cm,
故答案为:$\frac{16}{3}$.
点评 本题考查了直角三角形的性质,平行线的性质,熟练掌握直角三角形的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
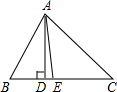 已知:如图,在△ABC中,∠B>∠C,AE为∠BAC的平分线,AD⊥BC于点D.求证:∠DAE=$\frac{1}{2}$(∠B-∠C)
已知:如图,在△ABC中,∠B>∠C,AE为∠BAC的平分线,AD⊥BC于点D.求证:∠DAE=$\frac{1}{2}$(∠B-∠C)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 600米 | B. | 800米 | C. | 1000米 | D. | 1300米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{0.5}$ | C. | $\sqrt{5}$ | D. | $\sqrt{50}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(+7)和+(-7) | B. | -(-7)与7 | C. | -|-1$\frac{1}{5}$|与-(-$\frac{6}{5}$) | D. | +(-$\frac{1}{100}$)与+(-0.01) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
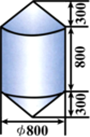 锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀100个这样的锚标浮筒需要用多少锌?(π取3.14,精确到0.1kg)
锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀100个这样的锚标浮筒需要用多少锌?(π取3.14,精确到0.1kg)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com