
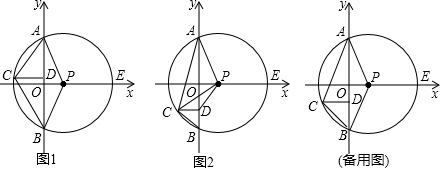
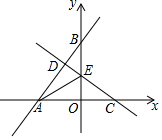
���� ��1����ͼ1�У�����PC��ֻҪ֤����APC�ǵȱ������μ��ɽ�����⣮
��2���������������ۢ���ͼ2�У���CD=2ADʱ���ӳ�CD����P��F����PH��CD��H������ͼ3�У���AD=2CDʱ���ӳ�CD����P��F����PH��CD��H���ֱ���⼴�ɣ�
��3����ͼ4�У�����PC��PD����PH��CD��CD���ӳ�����H���ɡ�AOP�ա�CHP���Ƴ�OP=PH��OA=CH=3����֤�ı���OPHD�������Σ�PO=PH=OD=DH=$\sqrt{{x}^{2}-9}$������S��PCD=$\frac{1}{2}$•CD•PH���㼴�ɽ�����⣮
��� �⣺��1����ͼ1�У�����PC��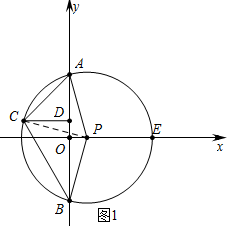
�ߡ�APC=2��ABC����ABC=30�㣬
���APC=60�㣬
��PA=PC��
���APC�ǵȱ������Σ�
��Rt��APO��PA=$\sqrt{O{A}^{2}+O{P}^{2}}$=$\sqrt{{6}^{2}+{1}^{2}}$=$\sqrt{37}$��
��AC=AP=$\sqrt{37}$��
��2������ͼ2�У���CD=2ADʱ���ӳ�CD����P��F����PH��CD��H��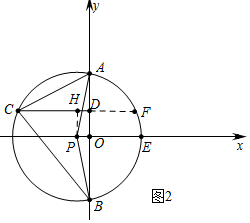
��AD=a����CD=2a��BD=3a��AB=4a��
��4a=12��
��a=3��
��CD=6��AD=3��DB=9��
��AD•DB=CD•DF��
��DF=$\frac{AD•DB}{CD}$=$\frac{9}{2}$��
��CF=CD+DF=$\frac{21}{2}$��
��PH��CF��
��CH=HF=$\frac{21}{4}$��
��DH=CD-CH=6-$\frac{21}{4}$=$\frac{3}{4}$��
��P��-$\frac{3}{4}$��0����
����ͼ3�У���AD=2CDʱ���ӳ�CD����P��F����PH��CD��H��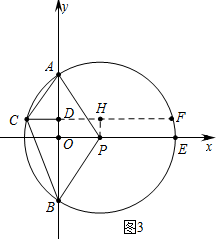
��AD=4a����CD=2a��BD=3a��AB=7a��
��7a=12��
��a=$\frac{12}{7}$��
��CD=$\frac{24}{7}$��AD=$\frac{48}{7}$��DB=$\frac{36}{7}$��
��AD•DB=CD•DF��
��DF=$\frac{AD•DB}{CD}$=$\frac{72}{7}$��
��CF=CD+DF=$\frac{96}{7}$��
��PH��CF��
��CH=HF=$\frac{48}{7}$��
��DH=CH-CD=$\frac{48}{7}$-6=$\frac{6}{7}$��
���P������$\frac{6}{7}$��0����
������������P������ΪP��-$\frac{3}{4}$��0����$\frac{6}{7}$��0����
��3����ͼ4�У�����PC��PD����PH��CD��CD���ӳ�����H��
�ߡ�CBD=45�㣬
���APC=2��ABC=90�㣬
���APC=��OPH��
���APO=��CPH����PA=PC����AOP=��PHC��
���AOP�ա�CHP��
��OP=PH��OA=CH=3����֤�ı���OPHD�������Σ�
��PO=PH=OD=DH=$\sqrt{{x}^{2}-9}$��
��S��PCD=$\frac{1}{2}$•CD•PH=$\frac{1}{2}$•��3-$\sqrt{{x}^{2}-9}$��•$\sqrt{{x}^{2}-9}$=$\frac{3}{2}$•$\sqrt{{x}^{2}-9}$-$\frac{1}{2}$x2+$\frac{9}{2}$��
��y=-$\frac{1}{2}$x2+$\frac{3}{2}$•$\sqrt{{x}^{2}-9}$+$\frac{9}{2}$����6��x��6$\sqrt{2}$����
���Ա�����ȡֵ��Χ��ȷ������Ҫ���ǡ�P��ֱ��y=-x-6�ڵ��������н��㼴�ɣ�
���� ���⿼��Բ�ۺ��⡢�ȱ������ε��ж������ʡ������������ཻ�Ҷ�����ȫ�������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п�ѹ���⣮


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
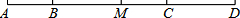 ��ͼ��B��C������߶�AD�ֳ�2��5��3�������֣�MΪAD���е㣬BM=9cm����CM��AD�ij���
��ͼ��B��C������߶�AD�ֳ�2��5��3�������֣�MΪAD���е㣬BM=9cm����CM��AD�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l1��y=$\frac{4}{3}$x+4�ֱ���x�ᡢy�ύ��A��B���㣬��CΪx��������һ�㣬ֱ��l2��y=-$\frac{3}{4}$x+b������C������ֱ��l1���ڵ�D����y�ύ�ڵ�E������AE��
��ͼ��ֱ��l1��y=$\frac{4}{3}$x+4�ֱ���x�ᡢy�ύ��A��B���㣬��CΪx��������һ�㣬ֱ��l2��y=-$\frac{3}{4}$x+b������C������ֱ��l1���ڵ�D����y�ύ�ڵ�E������AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{y}{2}-\frac{1}{4y}-3=0$ | B�� | $2y-\frac{1}{4y}-3=0$ | C�� | $2y-\frac{4}{y}-3=0$ | D�� | $\frac{y}{2}-\frac{4}{y}-3=0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��?ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����E��F�ֱ����߶�AO��BO���е㣬��AC+BD=22cm����OAB���ܳ���16cm����EF�ij�Ϊ2.5cm��
��ͼ��?ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����E��F�ֱ����߶�AO��BO���е㣬��AC+BD=22cm����OAB���ܳ���16cm����EF�ij�Ϊ2.5cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com