
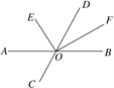
【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
【答案】(1)∠EOF=90°;(2) ∠AOC的度数变化时,∠EOF的度数不变化,理由见解析.
【解析】
(1)根据对顶角、邻补角,可得∠BOD、∠AOD,根据角平分线的性质,可得∠DOF与∠DOE的度数,根据角的和差,可得答案;
(2)根据角平分线的性质,可得∠DOF与∠DOE的度数,根据角的和差,可得答案.
(1)由对顶角相等,得∠BOD=∠AOC=50°,
由OF平分∠BOD,得∠DOF=![]() ∠BOD=
∠BOD=![]() ×50°=25°,
×50°=25°,
由邻补角互补,得∠AOD=180°-∠AOC=180°-50°=130°,
由OE平分∠AOD,得∠DOE=![]() ∠AOD=
∠AOD=![]() ×130°=65°,
×130°=65°,
由角的和差,得∠EOF=∠DOF+∠DOE=25°+65°=90°;
(2)∠AOC的度数变化时,∠EOF的度数不变化,
由OF平分∠BOD,得∠DOF=![]() ∠BOD,
∠BOD,
由OE平分∠AOD,得∠DOE=![]() ∠AOD,
∠AOD,
由角的和差,得∠EOF=∠DOF+∠DOE=![]() ∠BOD+
∠BOD+![]() ∠AOD=
∠AOD=![]() (∠AOD+∠BOD)=
(∠AOD+∠BOD)=![]() ∠AOB=90°.
∠AOB=90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】分解因式:
(1)a2b-abc; (2)3a(x-y)+9(y-x);
(3)(2a-b)2+8ab; (4)(m2-m)2+![]() (m2-m)+
(m2-m)+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人数) |
A | 80≤x<100 | 6 |
B | 100≤x<120 | 8 |
C | 120≤x<140 | m |
D | 140≤x<160 | 18 |
E | 160≤x<180 | 6 |
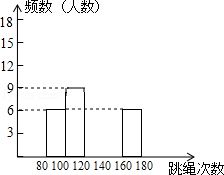
请结合图表解答下列问题:
(1)表中的m=;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. 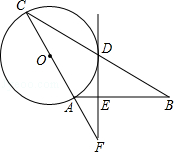
(1)求证:EF⊥AB;
(2)若∠C=30°,EF= ![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 ![]() 的坐标为
的坐标为![]() ,以 A 为顶点的
,以 A 为顶点的![]() 的两边始终与
的两边始终与 ![]() 轴交于
轴交于 ![]() 、
、![]() 两点(
两点(![]() 在
在 ![]() 左面),且
左面),且![]() .
.
(1)如图,连接![]() ,当
,当 ![]() 时,试说明:
时,试说明:![]() .
.

(2)过点 ![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,当
,当![]() 时,将
时,将![]() 沿
沿![]() 所在直线翻折,翻折后边
所在直线翻折,翻折后边![]() 交
交 ![]() 轴于点
轴于点 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点M的坐标为(2,8),点N的坐标为(2,6),将线段MN向右平移4个单位长度得到线段PQ(点P和点Q分别是点M和点N的对应点),连接MP、NQ,点K是线段MP的中点.
(1)求点K的坐标;
(2)若长方形PMNQ以每秒1个单位长度的速度向正下方运动,(点A、B、C、D、E分别是点M、N、Q、P、K的对应点),当BC与x轴重合时停止运动,连接OA、OE,设运动时间为t秒,请用含t的式子表示三角形OAE的面积S(不要求写出t的取值范围);
(3)在(2)的条件下,连接OB、OD,问是否存在某一时刻t,使三角形OBD的面积等于三角形OAE的面积?若存在,请求出t值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下列各数填入相应的集合中.
2,0,2π,![]() ,2018,﹣0.030030003…
,2018,﹣0.030030003…
有理数集合:{___________________________________________…};
无理数集合:{___________________________________________…};
非负整数集合:{_________________________________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是 ( )
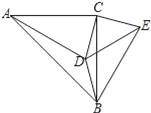
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com