
分析 (1)先把括号内的二次根式化为最简二次根式,然后合并后进行二次根式的除法运算;
(2)利用平方差公式计算.
解答 解:(1)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+3$\sqrt{3}$)÷$\sqrt{3}$
=$\frac{25\sqrt{3}}{3}$÷$\sqrt{3}$
=$\frac{25}{3}$;
(2)原式=11-13
=-2.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
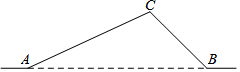 如图,从A地到B地的公路需经过C地,图中AC=50km,∠CAB=25°,∠CBA=45°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=50km,∠CAB=25°,∠CBA=45°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 476 | 604 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.6 | 0.59 | 0.604 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com