
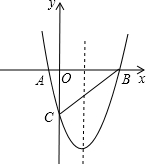
 在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.分析 (1)令y=0求出x值,结合点A在点B的左侧即可得出点A、B的坐标,再令x=0求出y值,即可得出点C的坐标;
(2)利用配方法找出抛物线的对称轴,设点P的坐标为(2,m),结合点A、C的坐标利用两点间的距离公式即可找出线段AC、AP、CP的长度,再根据勾股定理即可找出关于m的一元二次方程,解方程求出m值,由此即可得出点P的坐标;
(3)根据平行四边形的面积公式结合点O、B、E点的坐标即可得出S关于x的函数关系式,代入S=$\frac{175}{4}$求出x的值,根据点O、B的坐标即可得出点E在线段OB的垂直平分线上,此时?OEBF是菱形.
解答 解:(1)当y=0时,有x2-4x-5=0,
解得:x1=-1,x2=5,
∵点A在点B的左侧,
∴A(-1,0),B(5,0).
当x=0时,y=-5,
∴C(0,-5).
(2)∵y=x2-4x-5=(x-2)2-9,
∴抛物线的对称轴为x=2.
设点P的坐标为(2,m),
∵A(-1,0),C(0,-5),
∴AC=$\sqrt{[0-(-1)]^{2}+(-5-0)^{2}}$=$\sqrt{26}$,AP=$\sqrt{(-1-2)^{2}+(0-m)^{2}}$,CP=$\sqrt{(0-2)^{2}+(-5-m)^{2}}$.
∵AP⊥CP,
∴AC2=AP2+CP2,即m2+5m+6=0,
解得:m1=-3,m2=-2.
∴点P的坐标为(2,-3)或(2,-2).
(3)依照题意画出图形,如图所示.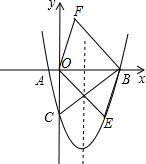
∵E(x,y)是抛物线对称轴右侧一动点,且位于第四象限,
∴E(x,x2-4x-5)(2<x<5),
∴S=OB•|yE|=-5x2+20x+25(2<x<5).
当S=$\frac{175}{4}$时,有-5x2+20x+25=$\frac{175}{4}$,
解得:x1=$\frac{3}{2}$(舍去),x2=$\frac{5}{2}$.
∵O(0,0),B(5,0),
∴当x=$\frac{5}{2}$时,点E在线段OB的垂直平分线上,
∴OE=BE,
∴此时?OEBF为菱形.
∴当?OEBF的面积为$\frac{175}{4}$时,?OEBF为菱形.
点评 本题考查了二次函数图象上点的坐标特征、二次函数的性质、勾股定理以及平行四边形的面积,解题的关键是:(1)根据二次函数图象上点的坐标特征求出点A、B、C的坐标;(2)根据勾股定理得出关于m的方程;(3)根据平行四边形的面积找出S关于x的函数关系式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
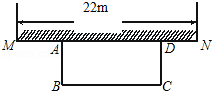 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用22m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用22m),现在已备足可以砌50m长的墙的材料.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
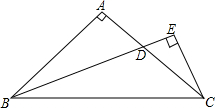 如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.
如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com